K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 1 2022
Bài 1:
a: \(=-10x^3+20x^4-5x\)
b: \(=\dfrac{1}{3}a^2b+7a^5-1\)
c: \(=a^3+8+25-a^3=33\)
d: \(=x^2-16+8-x^3=-x^3+x^2-8\)
e: \(=a^3+1+8-a^3=9\)
f: \(=\dfrac{7-2x+4x-8}{2x+3}=\dfrac{2x-1}{2x+3}\)
g: \(=\dfrac{3}{2\left(x+3\right)}-\dfrac{2}{x\left(x+3\right)}\)
\(=\dfrac{3x-4}{2x\left(x+3\right)}\)
KT
1
14 tháng 1
1: \(\dfrac{11}{x^4y};\dfrac{3}{xy^3}\)
\(\dfrac{11}{x^4y}=\dfrac{11\cdot y^2}{x^4y^3}=\dfrac{11y^2}{x^4y^3}\)
\(\dfrac{3}{xy^3}=\dfrac{3\cdot x^3}{xy^3\cdot x^3}=\dfrac{3x^3}{x^4y^3}\)
2: \(\dfrac{2}{3x^3y^2};\dfrac{3}{4x^7y}\)
\(\dfrac{2}{3x^3y^2}=\dfrac{2\cdot4\cdot x^4}{3x^3y^2\cdot4x^4}=\dfrac{8x^4}{12x^7y^2}\)
\(\dfrac{3}{4x^7y}=\dfrac{3\cdot3\cdot y}{4x^7y\cdot3y}=\dfrac{9y}{12x^7y^2}\)
22 tháng 10 2021
\(x\left(x+4\right)\left(x-4\right)-\left(x^2+1\right)\left(x^2-1\right)\)
\(=x\left(x^2-16\right)-\left(x^4-1\right)\)
\(=-x^4+x^3-16x+1\)
23 tháng 10 2021
\(a,=6x^5-15x^3-12x^2\\ b,=x^2+2x+1+x^2+x-6-4x=2x^2-x-5\\ c,=2x^2-3xy+4y^2\)
11 tháng 11 2021
Câu 6:
a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật
15 tháng 8 2021
b: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔAHB\(\sim\)ΔCAB
Suy ra: \(\dfrac{AB}{CB}=\dfrac{HB}{AB}\)
hay \(AB^2=BH\cdot BC\)
18 tháng 1 2022
a: \(=4x^2-x^4+8-2x^2=-x^4+2x^2+8\)
b: \(=\dfrac{x^2+x}{x+1}=x\)
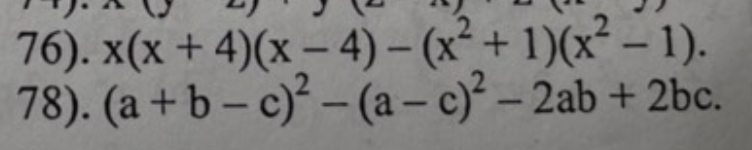
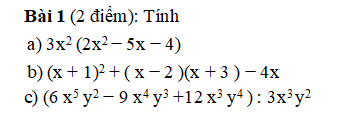
Giải gấp giúp em với. Giải từng câu và giải thích nhé ạ. Em cảm ơn
8) Ta có: \(x^2y+xy^2-4x-4y\)
\(=xy\left(x+y\right)-4\left(x+y\right)\)
\(=\left(x+y\right)\left(xy-4\right)\)
12) Ta có: \(a^2+2ab+b^2-ac-bc\)
\(=\left(a+b\right)^2-c\left(a+b\right)\)
\(=\left(a+b\right)\left(a+b-c\right)\)
10: Sửa đề: \(a^3-a^2x-ay+xy\)
Ta có: \(a^3-a^2x-ay+xy\)
\(=a^2\left(a-x\right)-y\left(a-x\right)\)
\(=\left(a-x\right)\left(a^2-y\right)\)