K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 8 2021
\(A\left(x\right)+B\left(x\right)=3x^4-4x^3+2x^2-3+8x^4+x^3-9x+\dfrac{2}{5}\)
\(=11x^4-3x^3+2x^2-9x-\dfrac{13}{5}\)
\(A\left(x\right)-B\left(x\right)=3x^4-4x^3+2x^2-3-8x^4-x^3+9x-\dfrac{2}{5}\)
\(=-5x^4-5x^3+2x^2+9x-\dfrac{17}{5}\)
\(B\left(x\right)-A\left(x\right)=8x^4+x^3-9x+\dfrac{2}{5}-3x^4+4x^3-2x^2+3\)
\(=5x^4+5x^3-2x^2-9x+\dfrac{17}{5}\)
4 tháng 8 2021
a) Ta có: \(P\left(x\right)=3x^5-2x^4-2x^5-2x^2-x+3x^2+2\)
\(=x^5-2x^4+x^2+2\)
Ta có: \(Q\left(x\right)=x^5+8-5x+3x^3+3x+x^4-4x^5\)
\(=-3x^5+x^4+3x^3-2x+8\)
b) \(P\left(x\right)+Q\left(x\right)=x^5-2x^4+x^2+2-3x^5+x^4+3x^3-2x+8\)
\(=-2x^5-x^4+3x^3+x^2-2x+10\)
\(P\left(x\right)-Q\left(x\right)=x^5-2x^4+x^2+2+3x^5-x^4-3x^3+2x-8\)
\(=4x^5-3x^4-3x^3+x^2+2x-6\)
2 tháng 9 2021
a: Ta có: \(\left(\dfrac{3}{5}-\dfrac{7}{4}\right):\dfrac{23}{10}\)
\(=\dfrac{12-35}{20}\cdot\dfrac{10}{23}\)
\(=\dfrac{-23\cdot10}{23\cdot20}=-\dfrac{1}{2}\)
b: Ta có: \(\left(-\dfrac{2}{3}+\dfrac{3}{4}\right)^2\cdot\dfrac{12}{5}-\dfrac{11}{5}\)
\(=\dfrac{1}{144}\cdot\dfrac{12}{5}-\dfrac{11}{5}\)
\(=\dfrac{1}{60}-\dfrac{11}{5}=\dfrac{1}{60}-\dfrac{132}{60}=\dfrac{-131}{60}\)
18 tháng 7 2021
a) Ta có: \(x-\dfrac{1}{2}=\left|\dfrac{3}{7}\right|\)
nên \(x-\dfrac{1}{2}=\dfrac{3}{7}\)
hay \(x=\dfrac{3}{7}+\dfrac{1}{2}=\dfrac{6}{14}+\dfrac{7}{14}=\dfrac{13}{14}\)
b) Ta có: |x-1|=0
nên x-1=0
hay x=1
c) Ta có: \(\left|x+1\right|\ge0\forall x\)
\(\left|y-2\right|\ge0\forall y\)
Do đó: \(\left|x+1\right|+\left|y-2\right|\ge0\forall x,y\)
Dấu '=' xảy ra khi x=-1 và y=2
18 tháng 7 2021
d) Ta có: \(\dfrac{x}{3}=\dfrac{y}{5}\)
mà x-y=-4
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x-y}{3-5}=\dfrac{-4}{-2}=2\)
Do đó: x=6; y=10
e) Ta có: 3x=4y
nên \(\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}\)
Đặt \(\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k\\y=\dfrac{1}{4}k\end{matrix}\right.\)
Ta có: xy=48
nên \(\dfrac{1}{3}k\cdot\dfrac{1}{4}k=48\)
\(\Leftrightarrow k^2\cdot\dfrac{1}{12}=48\)
\(\Leftrightarrow k^2=48\cdot12=576\)
hay \(k\in\left\{24;-24\right\}\)
Trường hợp 1: k=24
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k=\dfrac{1}{3}\cdot24=8\\y=\dfrac{1}{4}k=\dfrac{1}{4}\cdot24=6\end{matrix}\right.\)
Trường hợp 2: k=-24
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k=\dfrac{1}{3}\cdot\left(-24\right)=-8\\y=\dfrac{1}{4}k=\dfrac{1}{4}\cdot\left(-24\right)=-6\end{matrix}\right.\)
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
7 tháng 11 2021
a) \(\Rightarrow\left|\dfrac{3}{4}+x\right|=0\Rightarrow\dfrac{3}{4}+x=0\Rightarrow x=-\dfrac{3}{4}\)
b) \(\Rightarrow x+0,4=\dfrac{4}{9}:\dfrac{2}{3}=\dfrac{2}{3}\Rightarrow x=\dfrac{2}{3}-0,4=\dfrac{4}{15}\)
26 tháng 9 2021
Bài 8:
a: Ta có: \(\left(5x+1\right)^2=\dfrac{36}{49}\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+1=\dfrac{6}{7}\\5x+1=-\dfrac{6}{7}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{-1}{7}\\5x=\dfrac{-13}{7}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{35}\\x=\dfrac{-13}{35}\end{matrix}\right.\)
b: Ta có: \(\left(x-\dfrac{2}{9}\right)^3=\left(\dfrac{2}{3}\right)^6\)
\(\Leftrightarrow x-\dfrac{2}{9}=\dfrac{4}{9}\)
hay \(x=\dfrac{2}{3}\)
26 tháng 9 2021
\(7,\\ a,=\dfrac{3^{10}\cdot3^5\cdot5^5}{5^6\cdot\left[-\left(3^7\right)\right]}=\dfrac{3^8}{-5}=-\dfrac{6561}{5}\\ b,=8+3-\dfrac{1}{4}\cdot4+\left(4:\dfrac{1}{2}\right)\cdot8\\ =8+3-1+64=74\\ 8,\\ a,\left(5x+1\right)^2=\dfrac{36}{49}\Rightarrow\left[{}\begin{matrix}5x+1=\dfrac{6}{7}\\5x+1=-\dfrac{6}{7}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{35}\\x=-\dfrac{13}{35}\end{matrix}\right.\)
\(b,\Rightarrow8x-1=5\Rightarrow x=\dfrac{3}{4}\\ d,\Rightarrow\left\{{}\begin{matrix}x-3,5=0\\y-\dfrac{1}{10}=0\end{matrix}\right.\left[\left(x-3,5\right)^2\ge0;\left(y-\dfrac{1}{10}\right)^4\ge0\right]\\ \Rightarrow\left\{{}\begin{matrix}x=3,5\\y=\dfrac{1}{10}\end{matrix}\right.\)
10 tháng 11 2021
a)ABE = 180 độ - 35 độ = 145 độ
b) Vì DBC + BCy = 180 độ
=>Cy // DE
mà DE // Ax
=>Ax//Cy
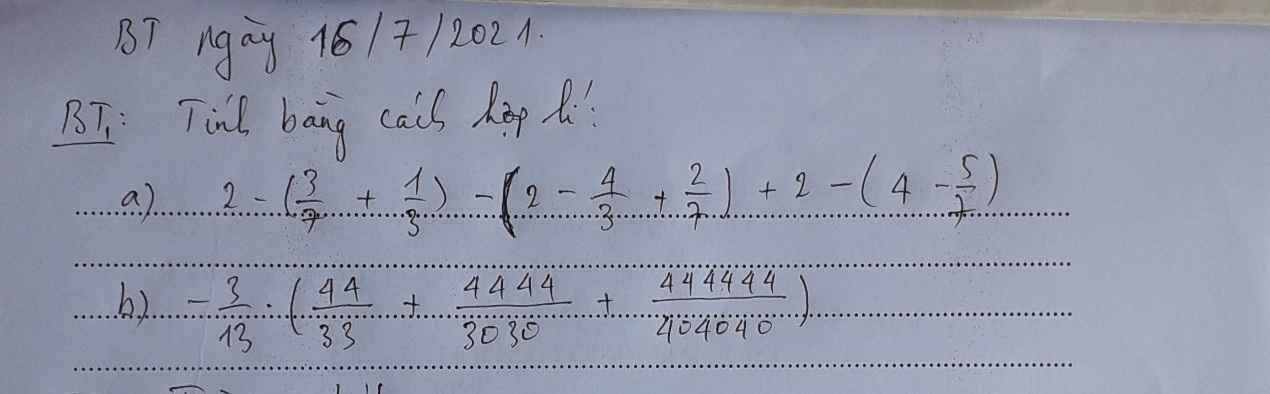
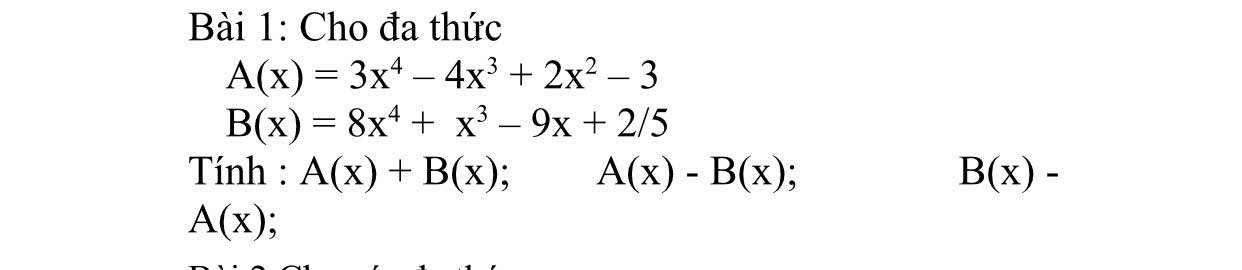
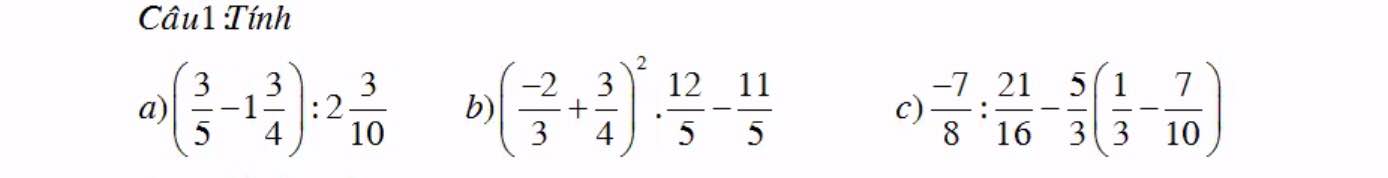
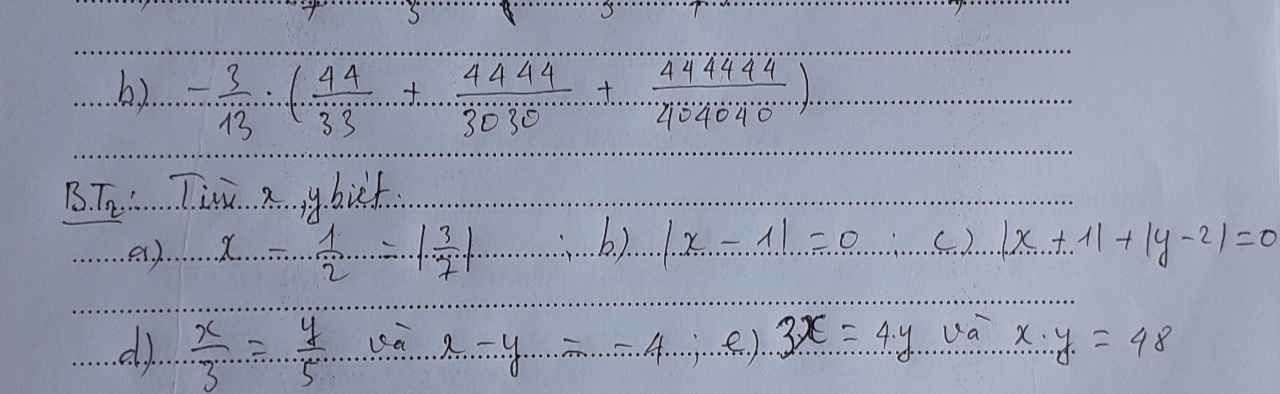
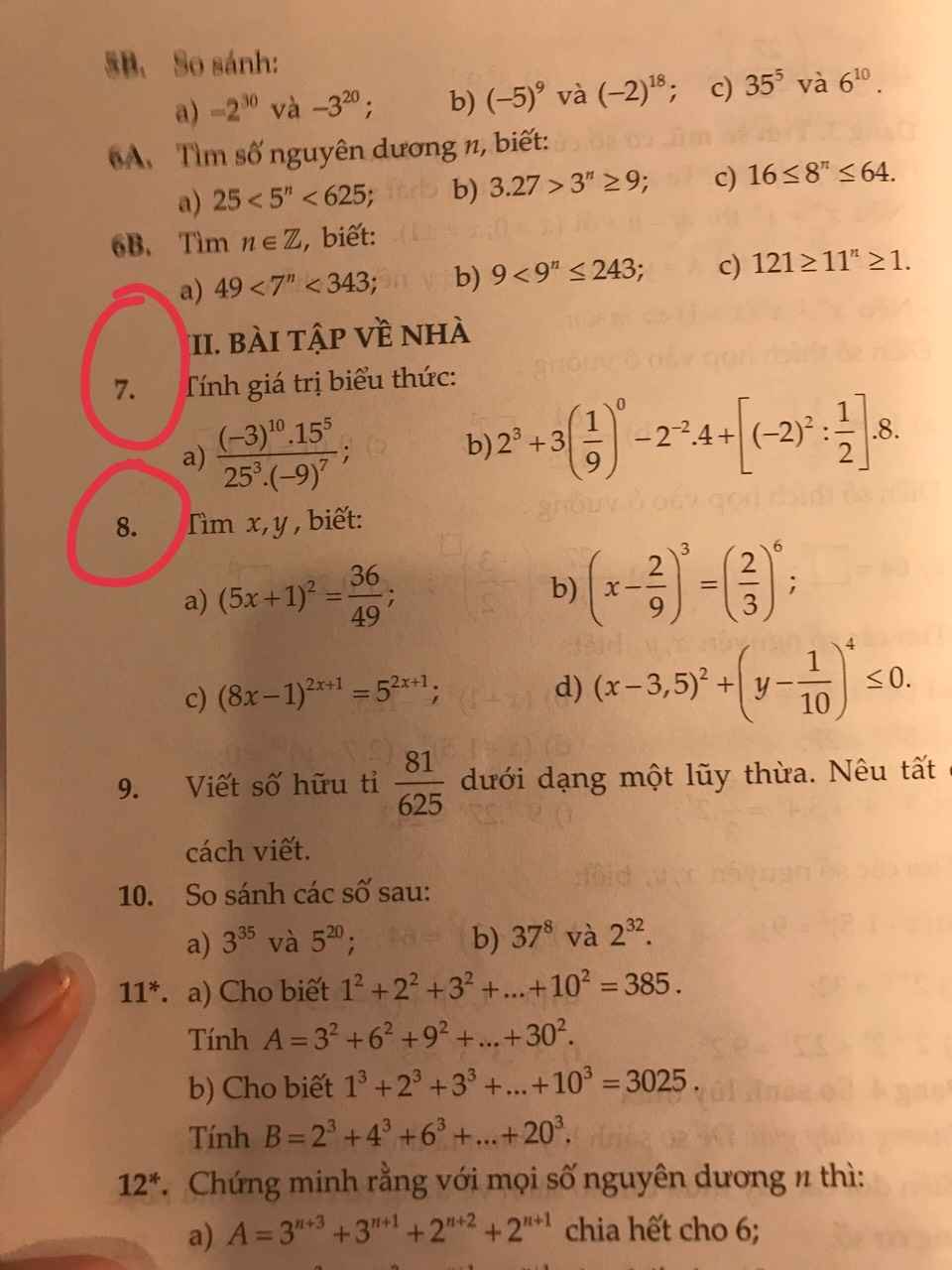
a) Ta có: \(2-\left(\dfrac{3}{7}+\dfrac{1}{3}\right)-\left(2-\dfrac{4}{3}+\dfrac{2}{7}\right)+2-\left(4-\dfrac{5}{7}\right)\)
\(=2-\dfrac{3}{7}-\dfrac{1}{3}-2+\dfrac{4}{3}-\dfrac{2}{7}+2-4+\dfrac{5}{7}\)
\(=-2\)
b) Ta có: \(\dfrac{-3}{13}\cdot\left(\dfrac{44}{33}+\dfrac{4444}{3030}+\dfrac{444444}{404040}\right)\)
\(=\dfrac{-3}{13}\left(\dfrac{4}{3}+\dfrac{22}{15}+\dfrac{11}{10}\right)\)
\(=\dfrac{-3}{13}\cdot\left(\dfrac{40}{30}+\dfrac{44}{30}+\dfrac{33}{30}\right)\)
\(=\dfrac{-3}{13}\cdot\dfrac{117}{30}\)
\(=\dfrac{-9}{10}\)