
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
\(\left(x^2+x\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}.\left(x^2\right)^{10-k}.x^k=\sum\limits^{10}_{k=0}C^k_{10}.x^{20-k}\)
\(\Rightarrow20-k=12\Rightarrow k=8\)
\(\Rightarrow\) Hệ số của \(x^{12}\) trong khai triển \(\left(x^2+x\right)^{10}\) là: \(C^8_{10}=45\)
2.
\(\left(x-\dfrac{1}{x}\right)^{13}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-k}.\dfrac{1}{x^k}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-2k}\)
\(\Rightarrow13-2k=7\Rightarrow k=3\)
\(\Rightarrow\) Hệ số của \(x^7\) trong khai triển \(\left(x-\dfrac{1}{x}\right)^{13}\) là: \(C^3_{13}=286\)

41.
Số hạng tổng quát của khai triển \(\left(x^2+x\right)^{10}\):
\(T_{k+1}=C^k_{10}.\left(x^2\right)^{10-k}.x^k=C^k_{10}.x^{20-k}\)
\(\Rightarrow20-k=12\Rightarrow k=8\)
\(\Rightarrow\) Hệ số của \(x^{12}\) trong khai triển \(\left(x^2+x\right)^{10}\) là: \(C^8_{10}\)

\(u_{n+1}=\sqrt{1+u_n^2}\left(1\right)\)
\(u_1=3=\sqrt{9}\)
\(u_2=\sqrt{1+u_1^2}=\sqrt{10}\)
\(u_3=\sqrt{1+u_2^2}=\sqrt{11}\)
...
Dự đoán công thức:\(u_n=\sqrt{n+8}\),\(n\ge1\) (*)
Thật vậy
+)\(n=1,(*)\)\(\Leftrightarrow u_1=3\) (lđ)
+)Giả sử (*) đúng với mọi \(n=k,k>1\)
\((*)\Leftrightarrow u_k=\sqrt{k+8}\)
+)\(n=k+1,\) thay vào (1) có: \(u_{k+2}=\sqrt{1+u^2_{k+1}}=\sqrt{1+\left(\sqrt{1+u_k^2}\right)^2}=\sqrt{2+u^2_k}=\sqrt{2+k+8}=\sqrt{10+k}\)
\(\Rightarrow\)(*) đúng với n=k+1
Vậy CTSHTQ: \(u_n=\sqrt{n+8}\), \(n\ge1\)

Đáp án B
Ta có u n = u n u n + 2
⇔ 1 u n = u n + 2 u n = 1 + 2 u n
Đặt v n = 1 u n ⇒ v 1 = 1 v n = 1 + 2 v n - 1
⇒ v n = 2 n - 1 ⇒ u n = 1 2 n - 1

Ta có :\(S_n=1^2+2^2+3^2+...+n^2=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}\left(n\in N^{\cdot}\right)\)
\(\Rightarrow S_{n-1}=1^2+2^2+3^2+...+\left(n-1\right)^2=\dfrac{\left(n-1\right)\left(n-1+1\right)\left(2n-2+1\right)}{6}=\dfrac{n\left(n-1\right)\left(2n-1\right)}{6}\)

\(u_{n+1}=\dfrac{2}{3}u_n+\dfrac{2}{3}\Rightarrow u_{n+1}-2=\dfrac{2}{3}\left(u_n-2\right)\)
Đặt \(u_n-2=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1-2=1\\v_{n+1}=\dfrac{2}{3}v_n\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội \(q=\dfrac{2}{3}\Rightarrow v_n=1.\left(\dfrac{2}{3}\right)^{n-1}=\left(\dfrac{2}{3}\right)^{n-1}\)
\(\Rightarrow u_n=v_n+2=\left(\dfrac{2}{3}\right)^{n-1}+2\)

* Ta có:
u 2 = 2 u 1 = 2.2 = 4 = 2 2 u 3 = 2 u 2 = 2.4 = 8 = 2 3 u 4 = 2 u 3 = 2.8 = 16 = 2 4 u 5 = 2 u 4 = 2.16 = 32 = 2 5
Từ các số hạng đầu tiên, ta dự đoán số hạng tổng quát u n có dạng: u n = 2 n ∀ n ≥ 1 ∗
* Ta dùng phương pháp chứng minh quy nạp để chứng minh cộng thức (*) đúng.
Với n=1 ; có: u 1 = 2 1 = 2 (đúng). Vậy (*) đúng với n= 1
Giả sử (*) đúng với n= k , có nghĩa ta có: u k = 2 k (2)
Ta cần chứng minh (*) đúng với n = k+1. Có nghĩa là ta phải chứng minh: u k + 1 = 2 k + 1 .
Thật vậy từ hệ thức xác định dãy số và theo (2) ta có:
u k + 1 = 2 u k = 2 . 2 k = 2 k + 1
Vậy (*) đúng với n = k+1. Kết luận (*) đúng với mọi số nguyên dương n.
Chọn đáp án B.

Ta có:
u 2 = u 1 + 2 = 3 + 2 = 5.
u 3 = u 2 + 2 = 5 + 2 = 7.
u 4 = u 3 + 2 = 7 + 2 = 9.
u 5 = u 4 + 2 = 9 + 2 = 11.
Từ các số hạng đầu trên, ta dự đoán số hạng tổng quát u n có dạng:
u n = 2 n + 1 ∀ n ≥ 1 ∗
Ta dùng phương pháp chứng minh quy nạp để chứng minh công thức (*) đúng.
Với n =1 ; u 1 = 2 . 1 + 1 = 3 (đúng). Vậy (*) đúng với n =1
Giả sử (*) đúng với n =k. Có nghĩa ta có: u k = 2 k + 1 (2)
Ta cần chứng minh (*) đúng với n = k+1 - có nghĩa là ta phải chứng minh:
u k + 1 = 2(k+1)+1= 2k + 3
Thật vậy từ hệ thức xác định dãy số và theo (2) ta có:
u k + 1 = u k +2 = 2k +1 +2 = 2k + 3
Vậy (*) đúng khi n = k+1 .
Kết luận (*) đúng với mọi số nguyên dương n.
Đáp án B
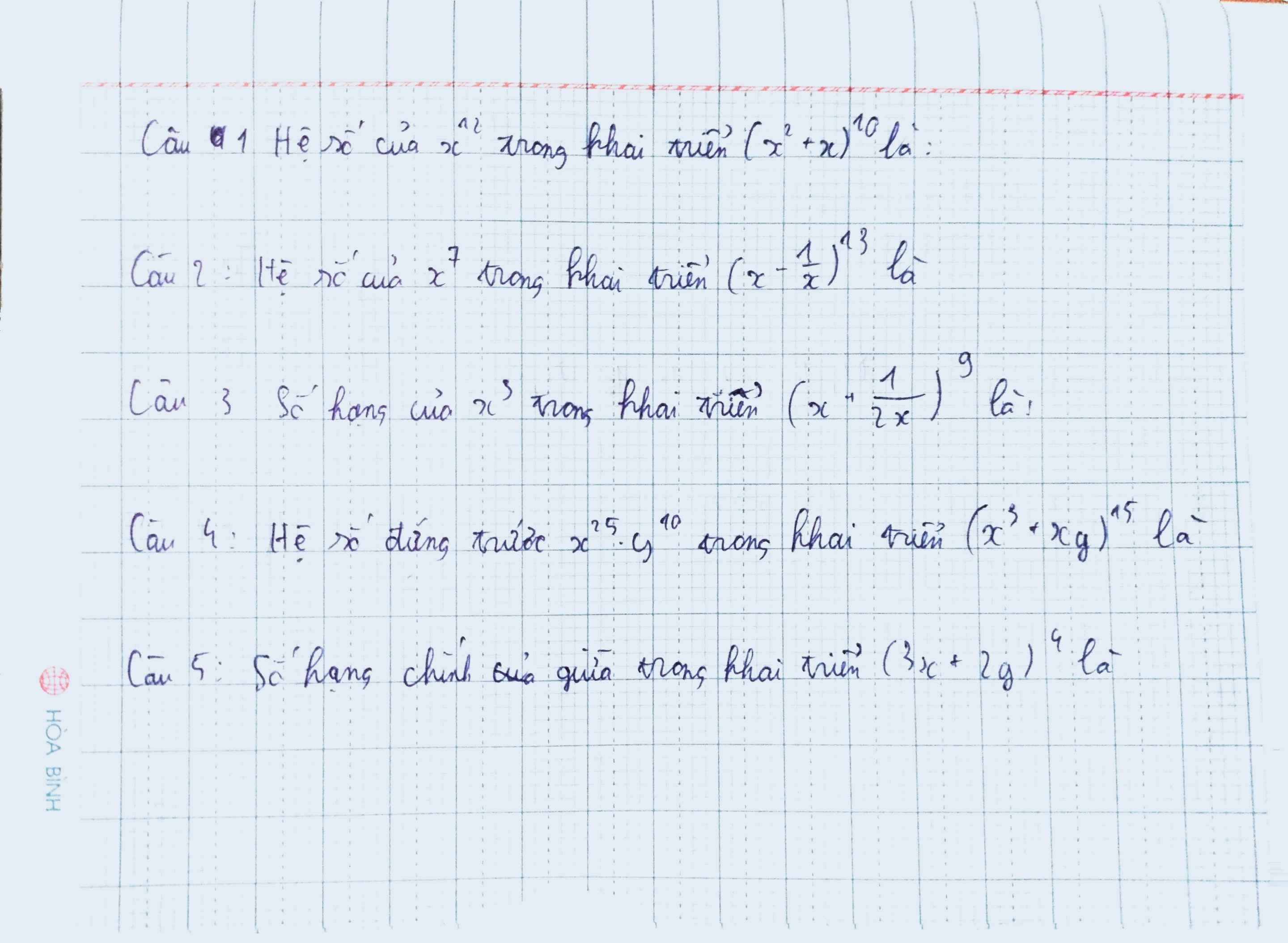

9.
Đặt \(u_n=2v_n\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{2015}{2}\\2v_{n+1}=8v_n^3-6v_n\end{matrix}\right.\) \(\Rightarrow v_{n+1}=4v_n^3-3v_n\)
Xét số thực a là nghiệm lớn hơn của pt:
\(a^2-2v_1a+1=0\Rightarrow\left\{{}\begin{matrix}a=v_1+\sqrt{v_1^2-1}\\\dfrac{1}{a}=v_1-\sqrt{v_1^2-1}\end{matrix}\right.\)
Khi đó ta có:
\(v_1=\dfrac{1}{2}\left(a+\dfrac{1}{a}\right)\)
\(v_2=4v_1^3-3v_1=4\left[\dfrac{1}{2}\left(a+\dfrac{1}{a}\right)\right]^3-3\left[\dfrac{1}{2}\left(a+\dfrac{1}{a}\right)\right]\)
\(=\dfrac{1}{2}\left(a^3+\dfrac{1}{a^3}\right)=\dfrac{1}{2}\left(a^{3^1}+\dfrac{1}{a^{3^1}}\right)\)
\(v_3=4v_2^3-3v_2=4\left[\dfrac{1}{2}\left(a^3+\dfrac{1}{a^3}\right)\right]^3-3\left[\dfrac{1}{2}\left(a^3+\dfrac{1}{a^3}\right)\right]=\dfrac{1}{2}\left(a^9+\dfrac{1}{a^9}\right)=\dfrac{1}{2}\left(a^{3^2}+\dfrac{1}{a^{3^2}}\right)\)
Từ đó, ta tổng quát được: \(v_n=\dfrac{1}{2}\left(a^{3^{n-1}}+\dfrac{1}{a^{3^{n-1}}}\right)\)
Ta chứng minh bằng quy nạp:
- Với \(n=1;2;3\) đúng như đã kiểm chứng ở trên
- Giả sử đúng với \(n=k\) hay \(v_k=\dfrac{1}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)\)
Ta cần chứng minh: \(v_{k+1}=\dfrac{1}{2}\left(a^{3^k}+\dfrac{1}{a^{3^k}}\right)\)
Ta có: \(v_{k+1}=4\left[\dfrac{1}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)\right]^3-3\left[\dfrac{1}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)\right]\)
\(=\dfrac{1}{2}\left(a^{3^k}+\dfrac{1}{a^{3^k}}\right)+\dfrac{3}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)-\dfrac{3}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)=\dfrac{1}{2}\left(a^{3^k}+\dfrac{1}{a^{3^k}}\right)\) (đpcm)
Vậy SHTQ của dãy là: \(u_n=2v_n=a^{3^{n-1}}+\dfrac{1}{a^{3^{n-1}}}\) với \(a\) là nghiệm lớn của pt: \(x^2-2015x+1=0\)
10.
Ta có: \(u_1=1=tan\dfrac{\pi}{4}=tan\dfrac{\pi}{2^2}\)
\(u_2=\dfrac{\sqrt{1+tan^2\dfrac{\pi}{4}}-1}{tan\dfrac{\pi}{4}}=\sqrt{2}-1=tan\dfrac{\pi}{8}=tan\dfrac{\pi}{2^3}\)
Dự đoán: \(u_n=tan\dfrac{\pi}{2^{n+1}}\)
Ta chứng minh bằng quy nạp
Với \(n=1;2\) đúng (đã kiểm chứng ở trên)
Giả sử điều đó đúng với \(n=k\) hay \(u_k=tan\dfrac{\pi}{2^{k+1}}\)
Ta cần chứng minh: \(u_{k+1}=tan\dfrac{\pi}{2^{k+2}}\)
Thật vậy, ta có:
\(u_{k+1}=\dfrac{\sqrt{1+u_k^2}-1}{u_k}=\dfrac{\sqrt{1+tan^2\dfrac{\pi}{2^{k+1}}}-1}{tan\dfrac{\pi}{2^{k+1}}}=\dfrac{\dfrac{1}{cos\dfrac{\pi}{2^{k+1}}}-1}{tan\dfrac{\pi}{2^{k+1}}}\)
\(=\dfrac{1-cos\dfrac{\pi}{2^{k+1}}}{sin\dfrac{\pi}{2^{k+1}}}=\dfrac{2sin^2\dfrac{\pi}{2^{k+2}}}{2sin\dfrac{\pi}{2^{k+2}}.cos\dfrac{\pi}{2^{k+2}}}=tan\dfrac{\pi}{2^{k+2}}\) (đpcm)