Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 3:
Ta có: a//b
nên \(x+y=180\)
mà \(2x-3y=0\)
nên \(\left\{{}\begin{matrix}x+y=180\\2x-3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+2y=180\\2x-3y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5y=180\\x+y=180\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=36\\x=144\end{matrix}\right.\)

\(1,\\ a,A_1=\left(x-2\right)^2+5\ge5\)
Dấu \("="\Leftrightarrow x=2\)
\(A_2=\left(x+1\right)^2+7\ge7\)
Dấu \("="\Leftrightarrow x=-1\)
\(A_3=\left(3-2x\right)^2-1\ge-1\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(A_4=\left(x-2\right)^2-3\ge-3\)
Dấu \("="\Leftrightarrow x=2\)
\(b,B_1=\left|x-2\right|+3\ge3\)
Dấu \("="\Leftrightarrow x=2\)
\(B_2=\left|x+1\right|+3\ge3\)
Dấu \("="\Leftrightarrow x=-1\)
\(B_3=\left|2x-4\right|-3\ge-3\)
Dấu \("="\Leftrightarrow x=2\)
\(B_4=\left|6x+1\right|-20\ge-20\)
Dấu \("="\Leftrightarrow x=-\dfrac{1}{6}\)
Bài 1:
a: \(A_1=\left(x-2\right)^2+5\ge5\forall x\)
Dấu '=' xảy ra khi x=2
\(A_2=\left(x+1\right)^2+7\ge7\forall x\)
Dấu '=' xảy ra khi x=-1
\(A_3=\left(3-2x\right)^2-1\ge-1\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
\(A_4=\left(x-2\right)^2-3\ge-3\forall x\)
Dấu '=' xảy ra khi x=2


a: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AC//BE và AC=BE
b: Xét tứ giác AIEK có
AI//KE
AI=KE
Do đó: AIEK là hình bình hành
Suy ra: Hai đường chéo AE và IK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AE
nên M là trung điểm của IK
hay I.M,K thẳng hàng



`7,`
`a, B+A=4x-2x^2+3`
`-> B=(4x-2x^2+3)-A`
`-> B=(4x-2x^2+3)-(x^2-2x+1)`
`B=4x-2x^2+3-x^2+2x-1`
`B=(-2x^2-x^2)+(4x+2x)+(3-1)`
`B=-3x^2+6x+2`
`b, C-A=-x+7`
`-> C=(-x+7)+A`
`-> C=(-x+7)+(x^2-2x+1)`
`-> C=-x+7+x^2-2x+1`
`C=x^2+(-x-2x)+(7+1)`
`C=x^2-3x+8`
`c,`
`A-D=x^2-2`
`-> D= A- (x^2-2)`
`-> D=(x^2-2x+1)-(x^2-2)`
`D=x^2-2x+1-x^2+2`
`D=(x^2-x^2)-2x+(1+2)`
`D=-2x+3`
`6,`
`a,`
`P+Q=4x-2x^2+3`
`-> Q=(4x-2x^2+3)-P`
`-> Q=(4x-2x^2+3)-(3x^2+x-1)`
`Q=4x-2x^2+3-3x^2-x+1`
`Q=(-2x^2-3x^2)+(4x-x)+(3+1)`
`Q=x^2+3x+4`
`b,`
`x^2-5x+2-P=H`
`-> H= (x^2-5x+2)-(3x^2+x-1)`
`H=x^2-5x+2-3x^2-x+1`
`H=(x^2-3x^2)+(-5x-x)+(2+1)`
`H=-4x^2-6x+3`
`c,`
`P-R=5x^2-3x-4`
`-> R= P- (5x^2-3x-4)`
`-> R=(3x^2+x-1)-(5x^2-3x-4)`
`R=3x^2+x-1-5x^2+3x+4`
`R=(3x^2-5x^2)+(x+3x)+(-1+4)`
`R=-2x^2+4x+3`


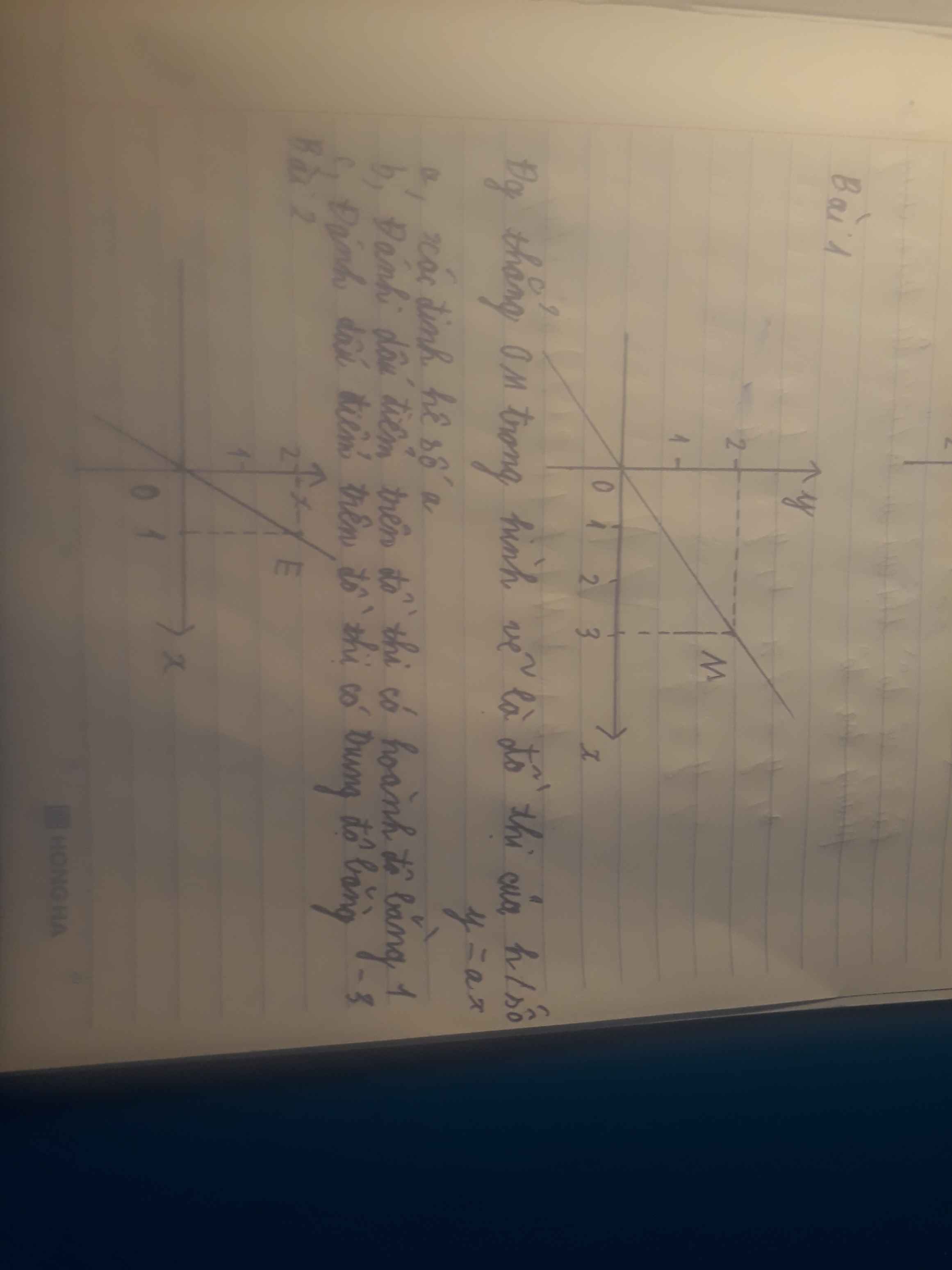


 Các bạn giúp mk mỗi bài 1 hoi ạ:))
Các bạn giúp mk mỗi bài 1 hoi ạ:))