n=5 a=8 Vậy nhaCâu trả lời: n=5 a=8 Vậy nha

giúp bài 2

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Nguễn Hồng Mỹy

24 tháng 2 2021 - olm

giúp bài 2

#Toán lớp 7

Lê Minh Đăng

24 tháng 2 2021

n=5 a=8 Vậy nha

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Thai Nguyen xuan

20 tháng 2 2022

Giúp e bài T^2 và 2) vs ạ,đc cả hai bài càng tốt còn nếu ko giúp e một bài cx đc ạ,giải chi tiết giúp e e c.ơn nhìu lắm

#Toán lớp 7

Nguyễn Lê Phước Thịnh

20 tháng 2 2022

Bài 2:

a: Ta có: ΔABC cân tại A

mà AH là đường cao

nên AH là tia phân giác của góc BAC

b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có

AH chung

\(\widehat{MAH}=\widehat{NAH}\)

Do đó: ΔAMH=ΔANH

Suy ra: AM=AN

hay ΔAMN cân tại A

c: Xét ΔABC có AM/AB=AN/AC

nên MN//BC

d: \(AH^2-AN^2=HN^2\)

\(BH^2-BM^2=MH^2\)

mà HN=MH

nên \(AH^2-AN^2=BH^2-BM^2\)

hay \(AH^2+BM^2=BH^2+AN^2\)

Đúng(0)

Thai Nguyen xuan

20 tháng 2 2022

Vẽ hình giúp e đc ko ạ

Đúng(0)

Bùi Quang Minh

10 tháng 3 2023

giúp em bài 1 ý 2, bài 2 và 4

#Toán lớp 7

Akai Haruma

Giáo viên

22 tháng 6 2023

Bài đâu hả bạn?

Đúng(0)

My Lai

22 tháng 4 2021

Giúp mình 1 trong 2 bài này với ạ. Nếu được thì giải 2 bài này giúp mk với. Mình đang cần gấp lắm ạ 😢

#Toán lớp 7

thu dinh

7 tháng 5 2021

jimmmmmmmmmmmmmmmmmmmmmmmmmmm

Đúng(0)

Male Libra ♎ ▬▬ι═══════ﺤ Ծ_Ծ ²ᵏ¹⁰...

16 tháng 6 2021

con cặc

he he he he he he

Đúng(1)

Hilo ddiw

4 tháng 3 2022

Giúp mik bài 1và bài 2 với

#Toán lớp 7

Nguyễn Lê Phước Thịnh

4 tháng 3 2022

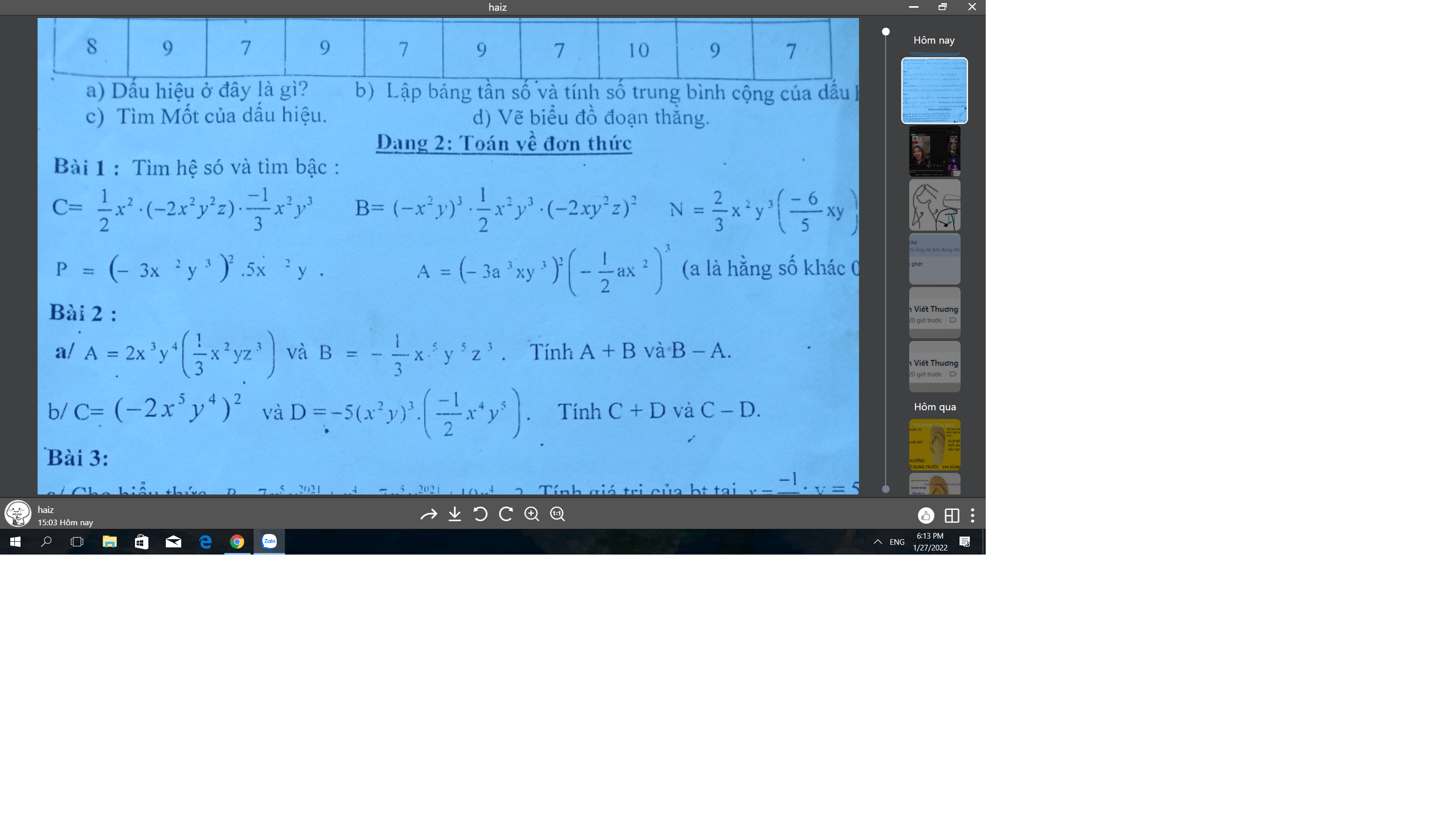
Bài 2:

\(A=\dfrac{-2}{3}x^2z\cdot\dfrac{-1}{8}xy^2z=\dfrac{1}{12}x^3y^2z^2\)

Bậc là 7

Hệ số là 1/12

Phần biến là \(x^3;y^2;z^2\)

Đúng(1)

qlamm

4 tháng 3 2022

ktra thì b tự lm đi chứ, mà còn là ktra giữa kì nữa

Đúng(1)

Thân

27 tháng 1 2022

giúp mk bài 2

giúp mình bài 2

#Toán lớp 7

Nguyễn Lê Phước Thịnh

27 tháng 1 2022

Bài 2:

a: \(A+B=\dfrac{2}{3}x^5y^5z^3-\dfrac{1}{3}x^5y^5z^3=\dfrac{1}{3}x^5y^5z^3\)

\(B-A=-\dfrac{1}{3}x^5y^5z^3-\dfrac{2}{3}x^5y^5z^3=-x^5y^5z^3\)

b: \(C+D=4x^{10}y^8+\dfrac{5}{2}x^{10}y^8=\dfrac{13}{2}x^{10}y^8\)

\(C-d=4x^{10}y^8-\dfrac{5}{2}x^{10}y^8=\dfrac{3}{2}x^{10}y^8\)

Đúng(1)

Châu Nguyễn Minh

16 tháng 8 2021

Giúp mình bài 1 và bài 2 với

#Toán lớp 7

ILoveMath

16 tháng 8 2021

Bài 1:

a) \(x^2-xy+x-y=\left(x^2-xy\right)+\left(x-y\right)=x\left(x-y\right)+\left(x-y\right)=\left(x^2+1\right)\left(x-y\right)\)

b) \(xz+yz-5\left(x+y\right)=\left(xz+yz\right)-5\left(x+y\right)=z\left(x+y\right)-5\left(x+y\right)=\left(x+y\right)\left(z-5\right)\)

c) \(3x^2-3xy-5x+5y=\left(3x^2-3xy\right)-\left(5x-5y\right)=3x\left(x-y\right)-5\left(x-y\right)=\left(x-y\right)\left(3x-5\right)\)

Đúng(1)

Nguyễn Lê Phước Thịnh

16 tháng 8 2021

Bài 1:

a: \(x^2-xy+x-y\)

\(=x\left(x-y\right)+\left(x-y\right)\)

\(=\left(x-y\right)\left(x+1\right)\)

b: \(xz+yz-5\left(x+y\right)\)

\(=z\left(x+y\right)-5\left(x+y\right)\)

\(=\left(x+y\right)\left(z-5\right)\)

c: \(3x^2-3xy-5x+5y\)

\(=3x\left(x-y\right)-5\left(x-y\right)\)

\(=\left(x-y\right)\left(3x-5\right)\)

Đúng(0)

nguyễn đăng khánh

16 tháng 11 2021

Giúp mình bài 1 và bài 2 với

#Toán lớp 7

Stick war 2 Order empire

16 tháng 2 2022

Giúp mik bài 1 và bài 2 với

#Toán lớp 7

Nguyễn Lê Phước Thịnh

17 tháng 2 2022

Bài 2:

Đặt AB=a; AC=b; BC=c

AB/AC=3/4

nên a/b=3/4

=>a=3/4b

Theo đề, ta có: \(a^2+b^2=c^2\)

\(\Leftrightarrow b^2\cdot\dfrac{25}{16}=225\)

=>b=12

=>a=9

Đúng(1)

Đặng Trần Gia Hân

21 tháng 12 2021

Mâý bạn giúp mình câu 1c với bài 2 giúp mình nha. Mình sắp nộp bài rồi ;-; mình cảm ơn nhiều!

#Toán lớp 7

Nguyễn Lê Phước Thịnh

21 tháng 12 2021

Bài 1:

a: Xét ΔABI và ΔACI có

AB=AC

AI chung

BI=CI

Do đó: ΔABI=ΔACI

Đúng(0)

Đặng Trần Gia Hân

21 tháng 12 2021

bạn làm được bài 1c ko ;-;

Đúng(0)

Abcdef

5 tháng 1 2022

Làm giúp mình bài 2 nha ko cần làm bài 1 đâu giúp mình thật chi tiết và đúng vs ạ

#Toán lớp 7

Nguyễn Lê Phước Thịnh

5 tháng 1 2022

Bài 2:

a: Xét ΔBHA vuông tại H và ΔBHD vuông tại H có

BH chung

HA=HD

Do đó: ΔBHA=ΔBHD

b: Ta có: ΔBHA=ΔBHD

nên \(\widehat{ABH}=\widehat{DBH}\)

hay BH là tia phân giác của góc ABD

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP