K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 8 2021
Bài 6:
a: Ta có: \(A=-x^2+2x+4\)
\(=-\left(x^2-2x+1-5\right)\)
\(=-\left(x-1\right)^2+5\le5\forall x\)
Dấu '=' xảy ra khi x=1
b: Ta có: \(B=-x^2+4x\)
\(=-\left(x^2-4x+4-4\right)\)
\(=-\left(x-2\right)^2+4\le4\forall x\)
Dấu '=' xảy ra khi x=2
T
14 tháng 9 2019
Đề có sai hem nhỉ? Nếu chỉ có dữ kiện như trên thì làm sao tam giác ABC cân được nhỉ? Bạn sửa lại đề nhanh nha!
N
14 tháng 9 2019
Cảm on tth vẽ giúp cái hình :))
Xet 2 tam giac AOD va tam giac BOC ta co:
AD=BC (hinh thang can 2 canh ben bang nhau)
\(\widehat{AOD}=\widehat{BOD}\) (doi dinh)
\(\widehat{DAC}=\widehat{BCA}\)(2 goc so le trong)
Do do;\(\Delta AOD=\Delta BOD\left(g-c-g\right)\)
Suy ra:\(OA=OB\)(2 canh tuong ung)
Hay \(\Delta AOB\)la tam giac can
Vi \(\Delta AOB\)la tam giac can nen:
\(\widehat{BAC}=\widehat{BDC}\)
16 tháng 11 2016
mình k biết làm nhưng bạn thử gõ lên google thử xem ! biết đâu sẽ có đấy :)
NX
31 tháng 8 2023
Ta có: \(\widehat{HAF}+\widehat{FAB}+\widehat{DAB}+\widehat{DAH}=360^o\)
Mà \(\widehat{FAB}=\widehat{DAH}=90^O\)
\(\Rightarrow\widehat{HAF}+\widehat{DAB}=180^o\)
Ta lại có: \(\widehat{ADC}+\widehat{DAB}=180^o\) ( 2 góc trong cùng phía nên kề bù với nhau )
\(\Rightarrow\widehat{HAF}=\widehat{ADC}\)
Xét \(\Delta HAF\) và \(\Delta ADC\) có:
\(HA=HD\left(gt\right)\)
\(\widehat{HAF}=\widehat{ADC}\left(CMT\right)\)
\(AF=DC\left(gt\right)\)
Vậy \(\Delta HAF\) \(=\) \(\Delta ADC\) \(\left(c.g.c\right)\)
\(\Rightarrow AC=FH\) ( 2 cạnh tưng ứng )
b) Ta có: \(\widehat{CBE}=\widehat{ABC}+90^o\)
\(\widehat{GDC}=\widehat{ADC}+90^o\)
Mà \(\widehat{ADC}=\widehat{ABC}\)
\(\Rightarrow\widehat{CBE}=\widehat{GDC}\)
Xét \(\Delta CBE\) và \(\Delta GDC\) ta có:
\(EB=CD\left(gt\right)\)
\(\widehat{CBE}=\widehat{GDC}\left(CMT\right)\)
\(CB=GD\left(gt\right)\)
Vậy \(\Delta CBE=\Delta GDC\left(c.g.c\right)\)
\(\Rightarrow CE=GC\) ( 2 cạnh tương ứng )
\(\Rightarrow\Delta CEG\) cân tại \(G\)
31 tháng 8 2023
a) Ta biết rằng trong hình bình hành ABCD, các đường chéo chia nhau đều và cắt nhau ở trung điểm.
Vì vậy, ta có AC = FH.
b) Vì ABFE là hình vuông, nên các cạnh AB và FE là song song và bằng nhau.
Tương tự, vì ADGH là hình vuông, nên các cạnh AD và GH cũng là song song và bằng nhau. Do đó, ta có AB || FE và AD || GH. Vì AC = FH (chứng minh ở câu a), và AB || FE, AD || GH,
nên theo tính chất của các đường song song, ta có AC || FH. Do đó, AC vuông góc với FH.
c) Ta biết rằng trong hình vuông, các đường chéo chia nhau đều và cắt nhau vuông góc.
Vì vậy, ta có AG ⊥ CE và CG ⊥ AE. Vì AG ⊥ CE, nên AGC là tam giác vuông tại G.
Vì CG ⊥ AE, nên CEG là tam giác vuông tại C. Vì AG = GC (vì AGC là tam giác vuông cân), nên ta cũng có CG = GC.
Do đó, ta có CEG là tam giác vuông cân.
Vậy, ta đã chứng minh được a), b), c) trong đề bài.
5 tháng 7 2023
1. =2.5xy x x^2y-2/5xy x 5x + 2/5xy x 10y
=2.5x^3y^2-2x^2y+4xy^2
mấy câu khác tương tự=))
H9
HT.Phong (9A5)
CTVHS
5 tháng 7 2023
1)
a, \(\dfrac{2}{5}xy\left(x^2y-5x+10y\right)\)
\(=\left(\dfrac{2}{5}xy\cdot x^2y\right)-\left(\dfrac{2}{5}xy\cdot5x\right)+\left(\dfrac{2}{5}xy\cdot10y\right)\)
\(=\dfrac{2}{5}x^3y^2-2x^2y+4xy^2\)
b, \(2x\left(x-3\right)+\left(x-2\right)\left(5-2x\right)\)
\(=2x^2-6x+5x-2x^2-10+4x\)
\(=3x-10\)
2)
a, \(3x^2y\left(x^2-3y+2xy^2\right)\)
\(=\left(3x^2y\cdot x^2\right)-\left(3x^2y\cdot3y\right)+\left(3x^2y\cdot2xy^2\right)\)
\(=3x^4y-9x^2y^2+6x^3y^3\)
b, \(\left(x-1\right)\left(x+2020\right)-\left(x+2019\right)\)
\(=x^2+2020x-x-2020-x-2019\)
\(=x^2+2018x-4039\)
3)
a, \(9x^2y\left(xy-2y+7xy^2\right)\)
\(=\left(9x^2y\cdot xy\right)-\left(9x^2y\cdot2y\right)+\left(9x^2y\cdot7xy^2\right)\)
\(=9x^3y^2-18x^2y^2+63x^3y^3\)
b, \(\left(x+1\right)^2+\left(x-1\right)^2-\left(x-1\right)\left(x+1\right)\)
\(=\left(x^2+2x+1\right)+\left(x^2-2x+1\right)-\left(x^2-1\right)\)
\(=x^2+2x+1+x^2-2x+1-x^2+1\)
\(=x^2+3\)
11 tháng 6 2019
Nếu y=0 thì pt trở thành:\(x^2-5x+6=0\)
\(\Leftrightarrow x^2-2x-3x+6=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow x=0;x=3\)
Nếu y=1 thì pt trở thành:\(x^2-5x+4=0\)
\(\Leftrightarrow x^2-x-4x+4=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-4\right)=0\)
\(\Leftrightarrow x=1;x=4\)
Nếu \(y\ge2\Rightarrow3^y⋮9\)
Do x là số tự nhiên nên x có dạng \(3k;3k+1;3k+2\) với \(k\in N\)
Với \(x=3k\) thì pt trở thành:
\(\left(3k\right)^2+5\cdot3k+7=3^y\left(KTM\right)\) vì VT không chia hết cho 3.
Với \(x=3k+1\) thì pt trở thành:
\(\left(3k+1\right)^2+5\cdot\left(3k+1\right)+7=3^y\)
\(\Leftrightarrow9k^2-9k+3=3^y\left(KTM\right)\) vì VT không chia hết cho 9.
Với \(x=3k+2\) thì pt trở thành:
\(\left(3k+2\right)^2+5\cdot\left(3k+2\right)+7=3^y\)
\(\Leftrightarrow9k^2-3k+1=3^y\left(KTM\right)\) vì VT không chia hết cho 3.
Vậy các cặp số tự nhiên \(\left(x;y\right)\) thỏa mãn là:\(\left(2;0\right);\left(3;0\right);\left(1;1\right);\left(4;1\right)\)
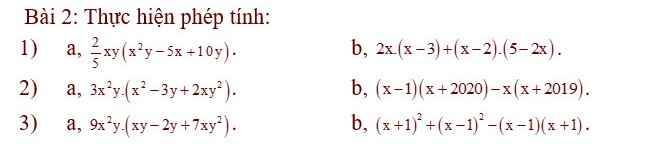
Trả lời:
Không có đề bài
Sao làm????