
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Lấy (1)+(2)+(3) là tìm được z rồi thế z vào tìm x, y
b) Lấy (1) + (2) - (3) là tìm được y
\(a)\hept{\begin{cases}x-2y+z=12\\2x-y+3z=18\\-3x+3y+2z=-9\end{cases}\Leftrightarrow\hept{\begin{cases}x-2y+z=12\\3y+z=-6\\6z=21\end{cases}}}\)
\(\text{Đáp số: }(x;y;z)=(\frac{16}{3};-\frac{19}{6};\frac{7}{2})\)
\(b)\hept{\begin{cases}x+y+z=7\\3x-2y+2z=5\\4x-y+3z=10\end{cases}\Leftrightarrow}\hept{\begin{cases}x+y+z=7\\-5y-z=16\\0y+0z=-2\end{cases}}\)
\(\text{ Hệ phương trình vô nghiệm.}\)


Gọi độ dài mỗi cạnh của tam giác lần lượt là x;y;z
Theo bài ra ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\) và x+y+z=72
theo tính chất dãy tỉ số bằng nhau ta có
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{72}{12}=6\)
=> x=18
y=24
z=30
Bài 21:
Gọi độ dài 3 cạnh của tam giác đó là: a, b, c ( a, b, c > 0 )
Theo đề bài, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và a + b + c = 72
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{72}{12}=6\)
Do đó:
\(\frac{a}{3}=6=>a=6\cdot3=18\)
\(\frac{b}{4}=6=>b=6\cdot4=24\)
\(\frac{c}{5}=6=>c=6\cdot5=30\)
Vậy độ dài 3 cạnh của tam giác đó theo thứ tự là: 18; 24; 30 ( cm ) thỏa mãn yêu cầu đề bài
Bài 22:
Gọi số học sinh 3 lớp 7A, 7B, 7C theo thứ tự là: a, b, c ( a, b, c thuộc N* )
Theo đề bài, ta có:
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}\) và c - a = 16
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{c-a}{6-4}=\frac{16}{2}=8\)
Do đó:
\(\frac{a}{4}=8=>a=8\cdot4=32\)
\(\frac{b}{5}=8=>b=8\cdot5=40\)
\(\frac{c}{6}=8=>c=8\cdot6=48\)
Vậy số học sinh 3 lớp 7A, 7B, 7C theo thứ tự là: 32; 40; 48 ( học sinh ) thỏa mãn yêu cầu đề bài





TỪ PT (1) TA CÓ
2X +20Y=60
=>X=(60-20Y)/2=30-10Y
THAY X=30-10Y VÀO PT (2) TA ĐƯỢC
((30-10Y)+3Y)2+((30-10Y)+11Y)2=1170
phần sau bạn tự giải nhé
k cần bài tuong tu nao hit, chỉ 5p giải lao giua 2 tiêt em lam giup a
thay x = -9-6y vào ta có:
(-9-6y +2y)2 + ( -9-6y +4y)2 =26
triển khai ta co pt: 5y2 + 27y + 34 = 0
dùng máy tính giải có: y1 = -2 ; y2 = -3,4
=> x1 = 3; x2= ...
( đã có đường đi đúng nhất định kq đ, thui em vào học r)
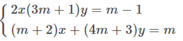
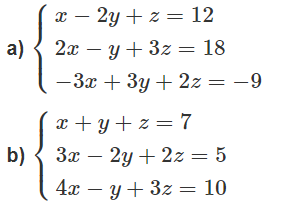 Giúp nhanh vs ạ, đng cần gấp
Giúp nhanh vs ạ, đng cần gấp
 và bài 22 giúp nhé
và bài 22 giúp nhé 






Nhân phương trình thứ nhất của hệ với m + 2, nhân phương trình thứ hai với 2 ta được hệ phương trình
Trừ hai phương trình vế theo vế ta được phương trình:
(3m2 - m - 4)y = (m + 1)(m + 2) (1)
+ Với m = -1 phương trình (1) có dạng: 0y = 0
Phương trình này nhận mọi giá trị thức của y làm nghiệm. Lúc đó thay m = -1 vào hệ phương trình đã cho, hai phương trình trở thành một phương trình.
x - y = 1 ⇒ y = x + 1, x tùy ý.
+ Với m = 4/3 phương trình (1) có dạng: 0y = -14/9
Phương trình này vô nghiệm, do đó hệ phương trình đã cho vô nghiệm.
+ Với m ≠ -1 và m ≠ 4/3, phương trình (1) có nghiệm duy nhất
Thay vào một trong hai phương trình của hệ đã cho ta suy ra
Kết luận
m = 4/3: Hệ phương trình đã cho vô nghiệm.
m = -1: Hệ phương trình đã cho có vô số nghiệm
x = a, y = a + 1, a là số thực tùy ý.
m ≠ 1, m ≠ 4/3: Hệ phương trình đã cho có nghiệm duy nhất :