
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LN
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên


10 tháng 7 2021
có 1 hình vuông và 2 hình chữ nhật
NH
0


6 tháng 2 2020
Gọi là đường thẳng đi qua
và song song với
và giả sử
.
 Vì
Vì là phân giác của
và
nên
.
Theo định lý Thales, ta có
Từ đó suy ra
Vậy theo định lý Ceva, các đường thẳng ,
và
đồng qu
PT
0

LT
16

7 tháng 9 2021
Đây là đáp án bài 2 nha bn tham khảo
do a chia cho 4, 5, 6 dư 1
nên (a - 1) chia hết cho 4, 5, 6
=> (a - 1) là bội chung của (4,5,6)
=> a - 1 = 60n
=> a = 60n+1 với 1 ≤ n < (400-1) / 60 = 6,65 mặt khác a chia hết cho 7
=> a = 7m
Vậy 7m = 60n + 1 có 1 chia 7 dư 1
=> 60n chia 7 dư 6 mà 60 chia 7 dư 4
=> n chia 7 dư 5 mà n chỉ lấy từ 1 đến 6
=> n = 5 a = 60.5 + 1 = 301
VN
2

17 tháng 2 2020
\(x^2+y^2=\left(x-y\right)\left(xy+2\right)+5\)tìm x,y biết x>y
 giúp mình với, toán lớp 5 tuổi nhưng cùng chủ đề với toán 8, hình chữ nhật và hình vuông
giúp mình với, toán lớp 5 tuổi nhưng cùng chủ đề với toán 8, hình chữ nhật và hình vuông
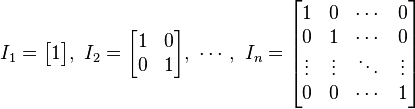
 Cứu cánh kịp thời đi mn
Cứu cánh kịp thời đi mn





ảnh dau