Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6 \)
Lại có: \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
\( \Rightarrow \)Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
Vậy diện tích tam giác ABC là 85,2.

Tham khảo:
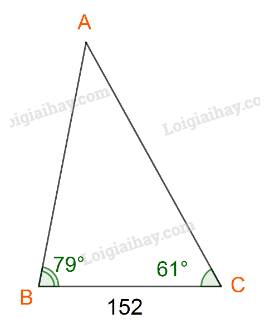
Đặt \(AB = c,AC = b,BC = a.\)
Ta có: \(a = 152;\widehat A = {180^o} - ({79^o} + {61^o}) = {40^o}\)
Áp dụng định lí sin, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Suy ra:
\(\begin{array}{l}AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{152.\sin {{79}^o}}}{{\sin {{40}^o}}} \approx 232,13\\AB = c = \frac{{a.\sin C}}{{\sin A}} = \frac{{152.\sin {{61}^o}}}{{\sin {{40}^o}}} \approx 206,82\\R = \frac{a}{{2\sin A}} = \frac{{152}}{{2\sin {{40}^o}}} \approx 118,235\end{array}\)

Tham khảo:

Đặt \(a = BC,b = AC,c = AB.\)
a) Áp dụng công thức \(S = \frac{1}{2}bc\sin A\), ta có: \({S_{ABC}} = \frac{1}{2}.8.6.\sin {60^o} = \frac{1}{2}.8.6.\frac{{\sqrt 3 }}{2} = 12\sqrt 3 \)
b) Áp dụng định lí cosin cho tam giác ABC ta được:
\(\begin{array}{l}B{C^2} = {a^2} = {8^2} + {6^2} - 2.8.6.\cos {60^o} = 52\\ \Rightarrow BC = 2\sqrt {13} \end{array}\)
Xét tam giác IBC ta có:
Góc \(\widehat {BIC} = 2.\widehat {BAC} = {120^o}\)(góc ở tâm và góc nội tiếp cùng chắn một cung)
\(IB = IC = R = \frac{a}{{2\sin A}} = \frac{{2\sqrt {13} }}{{2.\frac{{\sqrt 3 }}{2}}} = \frac{{2\sqrt {39} }}{3}.\)
\( \Rightarrow {S_{IBC}} = \frac{1}{2}.\frac{{2\sqrt {39} }}{3}.\frac{{2\sqrt {39} }}{3}\sin {120^o} = \frac{{13\sqrt 3 }}{3}.\)

Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
\( \Rightarrow c = \sin C.\frac{b}{{\sin B}} = \sin {45^o}.\frac{2}{{\sin {{30}^o}}} = 2\sqrt 2 \)
Lại có: \(\;\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {30^o} - {45^o} = {105^o}\)
Do đó diện tích tích S của tam giác ABC là:
\(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.2.2\sqrt 2 .\sin {105^o} = 1 + \sqrt 3 .\)
Vậy diện tích tam giác ABC là \(1 + \sqrt 3 \).

\(A=180-\left(B+C\right)=40^0\)
\(b=\dfrac{a}{sinA}.sinB\approx212.3\left(cm\right)\)
\(c=\dfrac{a}{sinA}.sinC=179,4\left(cm\right)\)
\(R=\dfrac{a}{2sinA}=107\left(cm\right)\)
\(S=\dfrac{abc}{4R}=12235,8\left(cm^2\right)\)

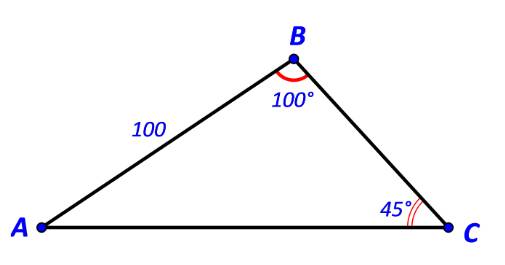
a)
Ta có: \(\widehat A = {180^o} - (\widehat B + \widehat C)\) \( \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
b)
Diện tích tam giác ABC là: \(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)

a) Áp dụng định lí cosin, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A\\ \Leftrightarrow {a^2} = {8^2} + {5^2} - 2.8.5.\cos {120^ \circ } = 129\\ \Rightarrow a = \sqrt {129} \end{array}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = \frac{8}{{\sin B}} = \frac{5}{{\sin C}}\\ \Rightarrow \left\{ \begin{array}{l}\sin B = \frac{{8.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,61\\\sin C = \frac{{5.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,38\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B \approx 37,{59^ \circ }\\\widehat C \approx 22,{41^ \circ }\end{array} \right.\end{array}\)
b) Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.8.5.\sin {120^ \circ } = 10\sqrt 3 \)
c)
+) Theo định lí sin, ta có: \(R = \frac{a}{{2\sin A}} = \frac{{\sqrt {129} }}{{2\sin {{120}^ \circ }}} = \sqrt {43} \)
+) Đường cao AH của tam giác bằng: \(AH = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{{\sqrt {129} }} = \frac{{20\sqrt {43} }}{{43}}\)

a) Áp dụng công thức: \(S = \frac{1}{2}bc\sin A\), ta có:
\(S = \frac{1}{2}.14.35.\sin {60^o} = \frac{1}{2}.14.35.\frac{{\sqrt 3 }}{2} \approx 212,2\)
Áp dụng đl cosin, ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
\(\begin{array}{l}
\Rightarrow {a^2} = {14^2} + {35^2} - 2.14.35.\cos {60^o} = 931\\
\Rightarrow a \approx 30,5
\end{array}\)
\( \Rightarrow R = \frac{a}{{2\sin A}} = \frac{{30,5}}{{2\sin {{60}^o}}} \approx 17,6\)
b) Ta có: \(p = \frac{1}{2}.(4 + 5 + 3) = 6\)
Áp dụng công thức Heron, ta có:
\(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {6(6 - 4)(6 - 5)(6 - 3)} = 6.\)
Lại có: \(S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{4.5.3}}{{4.6}} = 2,5.\)
Ta có: \(\widehat A = {15^o},\;\widehat B = {130^o} \Rightarrow \widehat C = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}\)
\( \Rightarrow b = \dfrac{{c.\sin B}}{{\sin C}};\;\;a = \dfrac{{c.\sin A}}{{\sin C}}\)
Mà \(\widehat A = {15^o},\;\widehat B = {130^o},\;\widehat C = {35^o},c = 6\)
\( \Rightarrow b = \dfrac{{6.\sin {{130}^o}}}{{\sin {{35}^o}}} \approx 8;\;\;a = \dfrac{{6.\sin {{15}^o}}}{{\sin {{35}^o}}} \approx 2,7\)
Diện tích tam giác ABC là \(S = \dfrac{1}{2}bc.\sin A = \dfrac{1}{2}.8.6.\sin {15^o} \approx 6,212.\)
Vậy \(a \approx 2,7;\;\,b \approx 8\); \(\widehat C = {35^o}\); \(S \approx 6,212.\)