
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
Biểu thức có nghĩa khi: $4-5x\geq 0\Leftrightarrow 4\geq 5x$
$\Leftrightarrow x\leq \frac{4}{5}$
Đáp án A.
Câu 2:
Căn bậc 2 số học của $13^2-12^2$ là $\sqrt{13^2-12^2}=\sqrt{25}=5$
Đáp án C
Câu 3: D (chắc mình không cần giải thích)
Câu 4:
$\sqrt[3]{-125}=\sqrt[3]{(-5)^3}=-5$
Đáp án B.
Câu 5:
$\sqrt{x-2}-3=0$
$\sqrt{x-2}=3$
$x-2=9$
$x=11$
Đáp án D.
Câu 6:
Đường thẳng đi qua gốc tọa độ thì có dạng: $y=ax$ với $a\in\mathbb{R}$
ĐT này cắt $(d)$ nên: $a\neq -1$
Đáp án C.

Câu 12.
\(5\sqrt{a}+6\sqrt{\dfrac{a}{4}}-a\sqrt{\dfrac{4}{a}}+5\sqrt{\dfrac{4a}{25}}\)
\(=5\sqrt{a}+6\dfrac{\sqrt{a}}{2}-a\cdot\dfrac{2}{\sqrt{a}}+5\dfrac{2\sqrt{a}}{5}\)
\(=5\sqrt{a}+3\sqrt{a}-2\sqrt{a}+2\sqrt{a}\) (vì a>0)
\(=8\sqrt{a}\)

Bài `13`
\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =\sqrt{9\cdot3}+\sqrt{16\cdot3}-\sqrt{36\cdot3}-\sqrt{4\cdot3}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =\left(3+4-6-2\right)\sqrt{3}\\ =-\sqrt{3}\\ b,\left(\sqrt{28}+\sqrt{12}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\\ =\left(\sqrt{4\cdot7}+\sqrt{4\cdot3}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{4\cdot21}\\ =\left(2\sqrt{7}+2\sqrt{3}-\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\\ =2\cdot7+2\sqrt{21}-7+2\sqrt{21}\\ =14+2\sqrt{21}-7+2\sqrt{21}\\ =7+4\sqrt{21}\)

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)


\(\sqrt{-x^2+2x-1}=\sqrt{-\left(x^2-2x+1\right)}=\sqrt{-\left(x-1\right)^2}\)
Do \(-\left(x-1\right)^2\le0\forall x\)
Nên căn thức chỉ xác định khi x=1

Do \(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{4}AC\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{6^2}=\dfrac{1}{\left(\dfrac{3}{4}AC\right)^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{36}=\dfrac{25}{9AC^2}\)
\(\Rightarrow AC=10\)
\(AB=\dfrac{3}{4}.AC=7,5\left(cm\right)\)
Áp dụng định lý Pitago: \(BC=\sqrt{AB^2+AC^2}=12,5\left(cm\right)\)
Hệ thức lượng:
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=4,5\left(cm\right)\)
\(CH=BC-BH=8\left(cm\right)\)
Ta có: AB:AC=3:4
nên \(AB=\dfrac{3}{4}AC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{3}{4}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{1}{6^2}=\dfrac{1}{36}\)
\(\Leftrightarrow\dfrac{1}{\dfrac{9}{16}AC^2}+\dfrac{\dfrac{9}{16}}{\dfrac{9}{16}AC^2}=\dfrac{1}{36}\)
\(\Leftrightarrow AC^2\cdot\dfrac{9}{16}=36\cdot\dfrac{25}{16}=\dfrac{225}{4}\)
\(\Leftrightarrow AC^2=100\)
hay AC=10(cm)
Ta có: \(AB=\dfrac{3}{4}AC\)
nên \(AB=\dfrac{3}{4}\cdot10=7.5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow BH^2=7.5^2-6^2=4.5^2\)
hay BH=4,5(cm)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow HC^2=10^2-6^2=64\)
hay HC=8(cm)
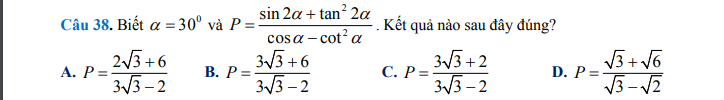







Chọn B
\(P=\dfrac{\sin60^0+\tan^260^0}{\cos30^0-\cot^230^0}=\dfrac{\dfrac{\sqrt{3}}{2}+3}{\dfrac{\sqrt{3}}{2}+3}=1\)
Do đó không có kết quả nào đúng hết