K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
30 tháng 8 2019
Đặt z = a + bi. Từ z + z = 3 + 4 i suy ra
⇒ a 2 + 16 = 3 - a 2 = 9 − 6a + a 2
⇒ 6a = −7 ⇒ a = −7/6
Vậy z = −7/6 + 4i
PT
1
CM
26 tháng 5 2017
a) Ta có z. z = z 2 nên từ z = z 3 ⇒ z 2 = z 4
Đặt z = a+ bi , suy ra:
a 4 + b 4 − 6 a 2 b 2 + 4ab( a 2 − b 2 )i = a 2 + b 2 (∗)
Do đó, ta có: 4ab( a 2 − b 2 ) = 0 (∗∗)
Từ (∗∗) suy ra các trường hợp sau:
+) a = b = 0 ⇒ z = 0
+) a = 0, b ≠ 0: Thay vào (∗), ta có b 4 = b 2 ⇒ b = 1 hoặc b = -1 ⇒ z = i hoặc z = -1
+) b = 0, a ≠ 0: Tương tự, ta có a = 1 hoặc a = -1 ⇒ z = 1 hoặc z = -1
+) a ≠ 0, b ≠ 0 ⇒ a 2 − b 2 = 0⇒ a 2 = b 2 , thay vào (∗) , ta có:
2 a 2 (2 a 2 + 1) = 0, không có a nào thỏa mãn (vì a ≠ 0 )
b) Đặt z = a + bi. Từ |z| + z = 3 + 4i suy ra
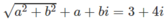
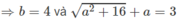
⇒ a 2 + 16 = ( 3 - a ) 2 = 9 − 6a + a 2
⇒ 6a = −7 ⇒ a = −7/6
Vậy z = −7/6 + 4i
23 tháng 7 2018
đặc \(z=a+bi\) (\(a;b\in R\) và \(i^2=-1\))
ta có : \(Y=3\left|z\right|+4\left|z-4i\right|+5\left|z-3\right|\)
\(\Leftrightarrow Y=3\left|a+bi\right|+4\left|a+\left(b-4\right)i\right|+5\left|\left(a-3\right)+bi\right|\)
\(\Leftrightarrow Y=3\sqrt{a^2+b^2}+4\sqrt{a^2+\left(b-4\right)^2}+5\sqrt{\left(a-3\right)^2+b^2}\)
áp dụng bất đẳng thức Bunhiacopxki ta có :
\(Y\ge-\sqrt{\left(3^2+4^2+5^2\right)\left(a^2+b^2+a^2+\left(b-4\right)^2+\left(a-3\right)^2+b^2\right)}\)
\(\Leftrightarrow Y\ge-5\sqrt{2}.\sqrt{3a^2+3b^2-8b-6a+25}\)
\(\Leftrightarrow Y\ge-5\sqrt{2}.\sqrt{3\left(a-1\right)^2+\left(\sqrt{3}b-\dfrac{8}{2\sqrt{3}}\right)^2+\dfrac{50}{3}}\)
dấu "=" xảy ra khi \(\dfrac{3}{\sqrt{a^2+b^2}}=\dfrac{4}{\sqrt{a^2+\left(b-4\right)^2}}=\dfrac{4}{\sqrt{\left(a-3\right)^2}+b^2}\)
giải ra tìm được \(a;b\) rồi thay ngược trở lại nha
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2023
\(z=x+yi\Rightarrow\sqrt{\left(x-3\right)^2+\left(y+4\right)^2}=\sqrt{x^2+y^2}\)
\(\Rightarrow6x-8y-25=0\)
\(\Rightarrow y=\dfrac{6x-25}{8}\)
\(\Rightarrow\left|z\right|=\sqrt{x^2+\left(\dfrac{6x-25}{8}\right)^2}=\dfrac{5}{8}\sqrt{\left(2x-3\right)^2+16}\ge\dfrac{5}{2}\)
Dấu "=" xảy ra khi \(x=\dfrac{3}{2};y=-2\Rightarrow z=\dfrac{3}{2}-2i\)
Không tồn tại \(\left|z\right|_{max}\)
goi \(z=a+bi\)
\(\Rightarrow\)\(\left|z\right|+z=3+4i\Leftrightarrow\sqrt{a^2+b^2}+a+bi=3+4i\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{a^2+b^2}+a=3\\b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}3-a\ge0\\a^2+b^2=\left(3-a\right)^2\end{matrix}\right.\\b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-7}{6}\\b=4\end{matrix}\right.\Rightarrow z=\dfrac{-7}{6}+4i\)
Cảm ơn bạn nhiều nha
