Question

[Nguyễn Thế Sơn]

Giải phương trình : \((x^2+x)^{2} + x^2 = (x+1)^2 \)

Answer 1

[Akai Haruma]

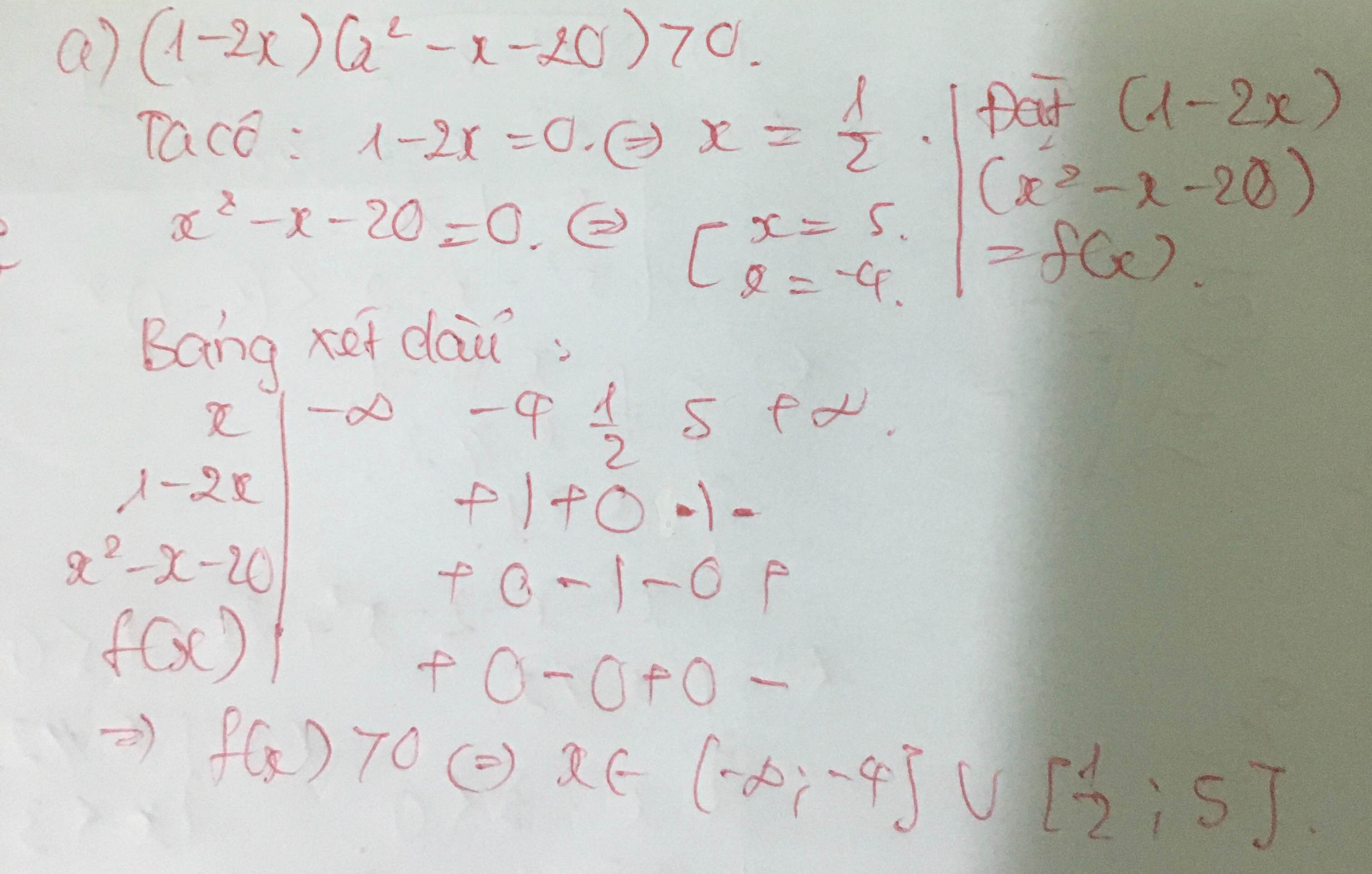
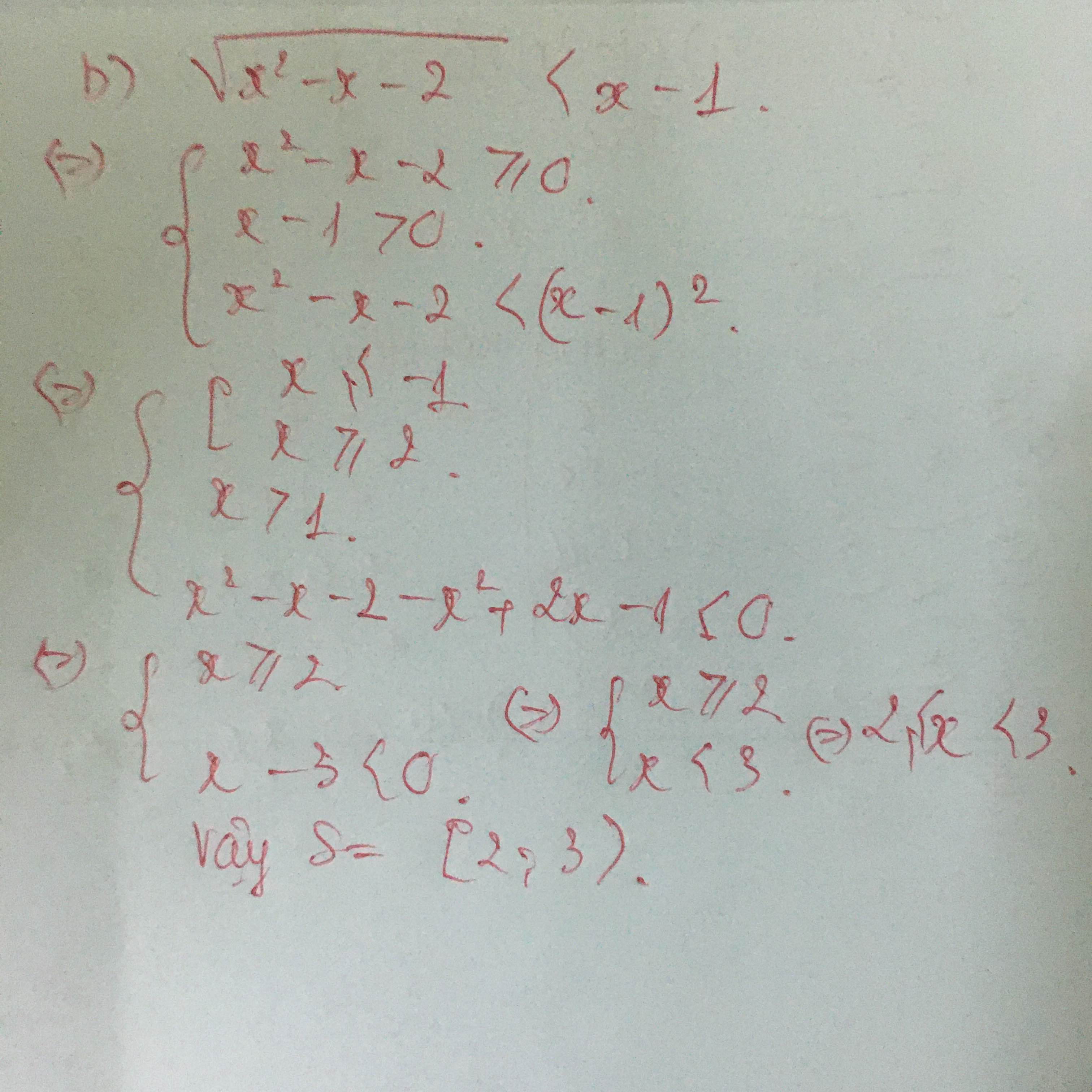
Lời giải:
Đặt $x=a; x+1=b$ thì ta có: \(\left\{\begin{matrix} b-a=1\\ a^2b^2+a^2=b^2\end{matrix}\right.\)

$\Rightarrow a^2b^2=(b-a)(b+a)$

$\Leftrightarrow a^2b^2=b+a$

$\Rightarrow a^4b^4=(a+b)^2=(a-b)^2+4ab=1+4ab$

Đặt $ab=t$ thì $t^4-4t-1=0$

$\Leftrightarrow (t^4+2t^2+1)-2(t^2+2t+1)=0$

$\Leftrightarrow (t^2+1)^2-2(t+1)^2=0$

$\Leftrightarrow (t^2+1-\sqrt{2}t-\sqrt{2})(t^2+1+\sqrt{2}t+\sqrt{2})=0$

$\Leftrightarrow t^2-\sqrt{2}t+1-\sqrt{2}=0$ hoặc $t^2+\sqrt{2}t+\sqrt{2}+1=0$

Do đó:

\(t=-\frac{\sqrt{2\sqrt{2}-1}-1}{\sqrt{2}}\) hoặc \(t=\frac{1+\sqrt{2\sqrt{2}-1}}{\sqrt{2}}\) 

Với \(t=ab=-\frac{\sqrt{2\sqrt{2}-1}-1}{\sqrt{2}}; b-a=1\), áp dụng định lý Viet đảo thì:

\(x=a=\frac{1}{2}(-1+\sqrt{2}-\sqrt{2\sqrt{2}-1})\)

Với \(t=ab=\frac{1+\sqrt{2\sqrt{2}-1}}{\sqrt{2}}; b-a=1\), áp dụng định lý Viet đảo thì:

\(x=a=\frac{1}{2}(-1+\sqrt{2}+\sqrt{2\sqrt{2}-1})\)