NT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PQ
1
13 tháng 1 2017
\(y\left(y-4\right)=192\Leftrightarrow y^2-4y+4=196\)\(\Leftrightarrow\left(y-2\right)^2=196=14^2\)
\(\orbr{\begin{cases}y-2=14\\y-2=-14\end{cases}\Rightarrow\orbr{\begin{cases}y=16\\y=-12\left(loai\right)\end{cases}}}\)\(\Rightarrow\orbr{\begin{cases}\left(x+1\right)=4\\\left(x+1\right)=-4\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\x=-5\end{cases}}}\)
KQ
1
NN
9 tháng 7 2019
( x2 - 1 ).( x2 + 4x + 3 ) = 192
\(\Leftrightarrow\) ( x - 1 ).( x + 1 ) .( x2 + 3x + x + 3 ) = 192
\(\Leftrightarrow\) ( x - 1 ).( x + 1 ).[ x.( x + 3 )+ ( x + 3 ) ] = 192
\(\Leftrightarrow\) ( x - 1 .( x + 1 ).( x + 1 ).( x + 3 ) -192 = 0
\(\Leftrightarrow\) ( x + 1 )2.( x - 1 ).( x +3 ) - 192 = 0
Đặt : x + 1 = a
Khi đó phương trình trở thành :
\(\Rightarrow\) a2.( a - 2 ).( a + 2 ) - 192 = 0
\(\Leftrightarrow\)a2.( a2 - 4 ) - 192 = 0
\(\Leftrightarrow\) a4 - 4a2 - 192 = 0
\(\Leftrightarrow\) ( a4 - 4a2 + 4 ) - 4 - 192 = 0
\(\Leftrightarrow\) ( a2 - 2 )2 - 196 = 0
\(\Leftrightarrow\)( a2 - 2 )2 - 142 = 0
\(\Leftrightarrow\)( a2 - 2 - 14 ).( a2 - 2 + 14 ) = 0
\(\Leftrightarrow\)( a2 - 16 ).( a2 + 12 ) = 0
\(\Leftrightarrow\) ( a - 4 ).( a + 4 ).( a2 + 12 ) = 0
\(\Leftrightarrow\) \(\orbr{\begin{cases}\left(a-4\right).\left(a+4\right)=0\\a^2+12=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}\left(a-4\right).\left(a+4\right)=0\\a^2=-12\left(vl\right)\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}a-4=0\\a+4=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}a=4\\a=-4\end{cases}}\)
Với a = 4 Với a = -4
\(\Rightarrow\) x + 1 = 4 \(\Rightarrow\) x + 1 = -4
\(\Leftrightarrow\) x = 3 \(\Leftrightarrow\) x = -5
Vậy phương trình có nghiệm là x = 3 , x = -5
13 tháng 11 2019
a) (x2 - 1)(x2 + 4x + 3) = 192
=> (x - 1)(x + 1)(x2 + x + 3x + 3) - 192 = 0
=> (x - 1)(x + 1)(x + 1)(x + 3) - 192 = 0
=> [(x - 1)(x + 3)](x + 1)2 - 192 = 0
=> (x2 + 2x - 3)(x2 + 2x + 1) - 192 = 0
Đặt x2 + 2x - 3 = k
=> k(k + 4) - 192 = 0
=> k2 + 4k - 192 = 0
=> k2 + 16k - 12k - 192 = 0
=> k(k + 16) - 12(k + 16) = 0
=> (k - 12)(k + 16) = 0
=> (x2 + 2x - 3 - 12)(x2 + 2x - 3 + 16) = 0
=> (x2 + 2x - 15)(x2 + 2x + 13) = 0
=> x2 + 5x - 3x - 15 = 0 (do x2 + 2x + 13 \(\ne\)0)
=> x(x + 5) - 3(x + 5) = 0
=> (x - 3)(x + 5) = 0
=> \(\orbr{\begin{cases}x-3=0\\x+5=0\end{cases}}\) => \(\orbr{\begin{cases}x=3\\x=-5\end{cases}}\)
13 tháng 11 2019
a) \(\left(x^2-1\right)\left(x^2+4x+3\right)=192\)
\(\Leftrightarrow x^4+4x^3+3x^2-x^2-4x-3=192\)
\(\Leftrightarrow x^4+4x^3+2x^2-4x-3=192\)
\(\Leftrightarrow x^4+4x^3+2x^2-4x-3-192=0\)
\(\Leftrightarrow x^4+4x^3+2x^2-4x-195=0\)
\(\Leftrightarrow\left(x^3+7x^2+23x+65\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left(x^2+2x+13\right)\left(x+5\right)\left(x-3\right)=0\)
mà \(x^2+2x+13\ne0\) nên:
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\x-3=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-5\\x=3\end{cases}}\)
CL
1
24 tháng 2 2017
(x² - 1)(x² + 4x + 3) = 192
<=> (x - 1)(x + 1)(x + 1)(x + 3) = 192
<=> (x - 1)(x + 3)(x + 1)² = 192
<=> (x² + 2x - 3)(x² + 2x + 1) = 192
Đặt t = x² + 2x + 1 => x² + 2x - 3 = t - 4
ta có pt: (t - 4)t = 192
<=> t² - 4t - 192 = 0
<=> t = - 12 hoặc t = 16
*t = x² + 2x + 1 = -12: vn
*t = x² + 2x + 1 = 16
<=> (x+1)² = 16
<=> x = -5 hoặc x = 3
Mãi mãi có một tương lai tươi sáng
20 tháng 9 2020
1) \(\frac{x-1}{x+3}-\frac{x}{x-3}=\frac{4x+15}{9-x^2}\)
ĐKXĐ : \(x\ne\pm3\)
\(\Leftrightarrow\frac{x-1}{x+3}-\frac{x}{x-3}=\frac{-4x-15}{x^2-9}\)
\(\Leftrightarrow\frac{\left(x-1\right)\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-\frac{x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{-4x-15}{\left(x-3\right)\left(x+3\right)}\)
\(\Leftrightarrow\frac{x^2-4x+3}{\left(x-3\right)\left(x+3\right)}-\frac{x^2+3x}{\left(x-3\right)\left(x+3\right)}=\frac{-4x-15}{\left(x-3\right)\left(x+3\right)}\)
\(\Leftrightarrow\frac{x^2-4x+3-x^2-3x}{\left(x-3\right)\left(x+3\right)}=\frac{-4x-15}{\left(x-3\right)\left(x+3\right)}\)
\(\Leftrightarrow-7x+3=-4x-15\)
\(\Leftrightarrow-7x+4x=-15-3\)
\(\Leftrightarrow-3x=-18\)
\(\Leftrightarrow x=6\)( tmđk )
Vậy x = 6 là nghiệm của phương trình
2) 2x + 3 < 6 - ( 3 - 4x )
<=> 2x + 3 < 6 - 3 + 4x
<=> 2x - 4x < 6 - 3 - 3
<=> -2x < 0
<=> x > 0
Vậy nghiệm của bất phương trình là x > 0
TT
1
7 tháng 2 2023
=>(2x-3)(2x+3)(x-4)-(2x-3)(x-4)(x+4)=0
=>(2x-3)(x-4)(2x+3-x-4)=0
=>(2x-3)(x-4)(x-1)=0
=>\(x\in\left\{1;4;\dfrac{3}{2}\right\}\)
T
21 tháng 4 2018
1
a (9+x)=2 ta có (9+x)= 9+x khi 9+x >_0 hoặc >_ -9
(9+x)= -9-x khi 9+x <0 hoặc x <-9
1)pt 9+x=2 với x >_ -9
<=> x = 2-9
<=> x=-7 thỏa mãn điều kiện (TMDK)
2) pt -9-x=2 với x<-9
<=> -x=2+9
<=> -x=11
x= -11 TMDK
vậy pt có tập nghiệm S={-7;-9}
các cau con lai tu lam riêng nhung cau nhan với số âm thi phan điều kiện đổi chiều nha vd
nhu cau o trên mk lam 9+x>_0 hoặc x>_0
với số âm thi -2x>_0 hoặc x <_ 0 nha
5 tháng 9 2021
a) \(x^2-4x+4=25\\ \Rightarrow\left(x-2\right)^2=25\\ \Rightarrow\left[{}\begin{matrix}x-2=-5\\x-2=5\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-3\\x=7\end{matrix}\right.\)
b) \(\left(5-2x\right)^2-16=0\\ \Rightarrow\left(5-2x\right)^2=16\\ \Rightarrow\left[{}\begin{matrix}5-2x=-4\\5-2x=4\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=4,5\\0,5\end{matrix}\right.\)
c) \(\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+9\left(x+1\right)^2=15\\ \Rightarrow\left(x-3\right)^3-\left(x-3\right)^3+9\left(x+1\right)^2=15\\ \Rightarrow9\left(x+1\right)^2=15\\ \Rightarrow\left(x+1\right)^2=\dfrac{5}{3}\\ \Rightarrow\left[{}\begin{matrix}x+1=-\sqrt{\dfrac{5}{3}}\\x+1=\sqrt{\dfrac{5}{3}}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{3+\sqrt{15}}{3}\\x=\dfrac{-3+\sqrt{15}}{3}\end{matrix}\right.\)
5 tháng 9 2021
a)\(\Leftrightarrow\)\(x^2-4x-21=0\)
\(\Leftrightarrow\)\(x^2-7x+3x-21=0\)
\(\Leftrightarrow\)\(x(x-7)+3(x-7)=0\)
\(\Leftrightarrow\)\((x-7)(x+3)=0\)
\(\Leftrightarrow\)\(\left[\begin{array}{} x=7\\ x=-3 \end{array} \right.\)
b)\(\Leftrightarrow\)\((5-2x)^2-4^2=0\)
\(\Leftrightarrow\)\((5-2x-4)(5-2x+4)=0\)
\(\Leftrightarrow\)\((-2x+1)(-2x+9)=0\)
\(\Leftrightarrow\)\(\left[\begin{array}{} x=\dfrac{1}{2}\\ x=\dfrac{9}{2} \end{array} \right.\)
PT
1
CM
25 tháng 7 2018
⇔ 
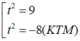
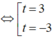
Với t = 3 ⇒ x = - 1/2
Với t = - 3 ⇒ x = - 5/4
Vậy tập nghiệm của phương trình là S = { - 1/2; - 5/4 }
Mình xin phép sửa đề bài này vì đề của bạn không có khả năng tìm ra nghiệm thông thường và nghiệm xấu
Ta có: \(\left(x^2-1\right)\left(x^2+4x+3\right)=192\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+1\right)\left(x+3\right)=192\)
\(\Leftrightarrow\left(x^2+2x-3\right)\left(x^2+2x+1\right)=192\)
Đặt \(x^2+2x-1=a\)
\(PT\Leftrightarrow\left(a-2\right)\left(a+2\right)=192\)
\(\Leftrightarrow a^2-4=192\Leftrightarrow a^2=196\Rightarrow\orbr{\begin{cases}a=14\\a=-14\end{cases}}\)
TH1: \(a=14\Leftrightarrow x^2+2x-1=14\Leftrightarrow x^2+2x-15=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+5\right)=0\Leftrightarrow\orbr{\begin{cases}x=3\\x=-5\end{cases}}\)
TH2: \(a=-14\Leftrightarrow x^2+2x-1=-14\Leftrightarrow\left(x+1\right)^2=-12\)
=> PT vô nghiệm
Vậy x = 3 hoặc x = -5
dạ camon