K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
N
11 tháng 1 2019
\(\left(x^2-2.3.x+9\right)+\left(y^2+2.5.y+25\right)=58\)
\(\Leftrightarrow\left(x-3\right)^2+\left(y+5\right)^2=58\)
vì \(\hept{\begin{cases}\left(x-3\right)^2\ge0\\\left(y+5\right)^2\ge0\end{cases}\text{và là hai số chính phương}}\)
mà 58 chẵn => \(\hept{\begin{cases}\left(x-3\right)^2\\\left(y+5\right)^2\end{cases}\text{cùng tính chẵn lẻ}}\)
tự c/m nha, bn xét SCP chẵn, lẻ là đc(ko c/m đc ib)
\(\text{mà chỉ có 49, 9 t/m điều kiện }\Rightarrow...\)
NT
0
K
1
S
11 tháng 1 2019
\(x^2-6x+y^2+10y=24\)
\(\Leftrightarrow x^2-6x+9+y^2+10x+25=58\Leftrightarrow\left(x-3\right)^2+\left(y+5\right)^2=58\)
\(\Leftrightarrow\left(x-3\right)^2\le58\Leftrightarrow\left(x-3\right)^2\in\left\{0;1;4;9;16;25;36;49\right\}\)
Dễ nhận thấy chỉ có tổng của 49 và: 9; 9 và 49 thỏa mãn (vì các số trên là số chính phương
\(\Rightarrow\orbr{\begin{cases}\hept{\begin{cases}\left(x-3\right)^2=49\Leftrightarrow x-3=7\Leftrightarrow x=10\\\left(y+5\right)^2=9\Leftrightarrow y+5=3\Leftrightarrow y=-2\end{cases}}\\\end{cases}}\)<=> (x-3)^2+(y+5)^2=49+9=9+49
+) (x-3)^2+(y+5)^2=49+9
=> x-3=7=>x=10 và: y+5=3=>y=-2
+) (x-3)^2+(y+5)^2=9+49
=> (x-3)=3=>x=6 và y+5=7=>y=2
Vậy có 2 cặp (x,y)={(6;2);(10;-2)}
thỏa mãn điều kiện
NW
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 1
\(\Leftrightarrow x^4-4x^3+12x^2-32x+32=\left(y-5\right)^2\)
\(\Leftrightarrow\left(x-2\right)^2\left(x^2+8\right)=\left(y-5\right)^2\)
- Với \(x=2\Rightarrow y=5\)
- Với \(x\ne2\Rightarrow x-2\) là ước của \(y-5\)
Đặt \(y-5=n\left(x-2\right)\)
\(\Rightarrow\left(x-2\right)^2\left(x^2+8\right)=n^2\left(x-2\right)^2\)
\(\Rightarrow x^2+8=n^2\)
\(\Rightarrow\left(n-x\right)\left(n+x\right)=8\)
\(\Rightarrow\left[{}\begin{matrix}x=1;n=-3\Rightarrow y=8\\x=-1;n=-3\Rightarrow y=14\\x=1;n=3\Rightarrow y=2\\x=-1;n=3\Rightarrow y=-4\end{matrix}\right.\)
PT
1
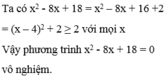
=>10y=18-8x
=>y=(9-4x)/5