K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VA
13 tháng 1 2017
Theo đề bài ta có: a3 + b3 = c3
Suy ra: (a + b)3 = c3
Vậy a,b,c = 1 hoặc a,b,c = 0
VN
23 tháng 2 2017
O x y C B A
(Vẽ có thể chưa chuẩn, thêm kí hiệu bằng nhau cho góc \(\widehat{xOc}\)và \(\widehat{cOy}\)vì \(OC\)là phân giác)
a/ Vì \(OC\)là phân giác \(\widehat{xOy}\Rightarrow\widehat{xOc}=\widehat{cOy}\)
\(\Rightarrow\)Khoảng cách từ \(C\)đến \(OA\)( Chính là \(CA\)) sẽ bằng khoảng cách từ \(C\)đến \(OB\)( Chính là \(CB\))
\(\Rightarrow CA=CB\left(đpcm\right)\)
b/ Xét \(\Delta ACD\)và \(\Delta BCE\)có:
\(\widehat{ACD}=\widehat{BCE}\)(đối đỉnh)
\(CA=CB\)(Chứng minh câu a)
\(\widehat{DAC}=\widehat{EBC}=90\)độ
\(\Rightarrow\Delta ACD=\Delta BCE\left(g.c.g\right)\)
\(\Rightarrow CD=CE\)(hai cạnh tương ứng)
19 tháng 9 2018
=> 1 - 3 . X=x - 7 hoặc 1 - 3 . X =-(x-7)
*1 - 3x =x - 7 *1 - 3x = -(x - 7 )
8 =x + 3x 1 - 3x = -x + 7
8 =4x -3x+x =7-1
8 : 4 =x -2x =6
2 = x x = 6:(-2)
=>x = 2 x = -3
vậy x \(\in\){2; -3}
đúng + x =1
x =1 -đúng
x = thích
28 tháng 10 2023
a) \(\left(\dfrac{1}{3}\right)^m=\dfrac{1}{81}\)
\(\Rightarrow\left(\dfrac{1}{3}\right)^m=\left(\dfrac{1}{3}\right)^4\)
\(\Rightarrow m=4\)
b) \(\dfrac{1}{9}\cdot27^n=3^n\)
\(\Rightarrow\dfrac{1}{3^2}\cdot\left(3^3\right)^n=3^n\)
\(\Rightarrow\dfrac{3^{3n}}{3^2}=3^n\)
\(\Rightarrow3^{3n-2}=3^n\)
\(\Rightarrow3n-2=n\)
\(\Rightarrow2n=2\)
\(\Rightarrow n=1\)
c) \(\dfrac{8}{2^n}=2\)
\(\Rightarrow\dfrac{2^3}{2^n}=2\)
\(\Rightarrow2^{3-n}=2^1\)
\(\Rightarrow3-n=1\)
\(\Rightarrow n=2\)
d) \(32^n\cdot16^{-n}=1024\)
\(\Rightarrow\left(2^5\right)^n\cdot\left(2^4\right)^{-n}=2^{10}\)
\(\Rightarrow2^{5n-4n}=2^{10}\)
\(\Rightarrow2^n=2^{10}\)
\(\Rightarrow n=10\)
e) \(3^{-1}\cdot3^n+5\cdot3^{n-1}=162\)
\(\Rightarrow3^{n-1}+5\cdot3^{n-1}=162\)
\(\Rightarrow3^{n-1}\cdot6=162\)
\(\Rightarrow3^{n-1}=27\)
\(\Rightarrow3^{n-1}=3^3\)
\(\Rightarrow n-1=3\)
\(n=4\)
f) \(\left(n-\dfrac{2}{3}\right)^3=\dfrac{1}{27}\)
\(\Rightarrow\left(n-\dfrac{2}{3}\right)^3=\left(\dfrac{1}{3}\right)^3\)
\(\Rightarrow n-\dfrac{2}{3}=\dfrac{1}{3}\)
\(\Rightarrow n=\dfrac{1}{3}+\dfrac{2}{3}\)
\(\Rightarrow n=1\)
30 tháng 10 2018
Cho em xin đề toan hình 1 tiết lớp 7 với ạ !! Em cần gấp !!!!!!! Mọi người giúp em !! Rồi giải câu đó ra cho em luôn ạ !! EM cảm ơn nhiều <3
30 tháng 10 2018
Câu 1:(1,5 điểm)
Trong hình sau, cho a // b tính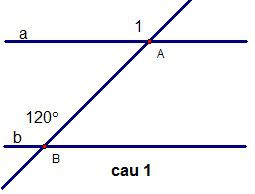 
Câu 2:(1,5 điểm)
Cho đoạn thẳng AB dài 3cm. Vẽ đường trung trực của đoạn thẳng AB.
Câu 3:(3 điểm)
Cho a // b; c 
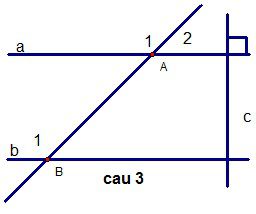
Đường thẳng c có vuông góc với đường thẳng b không ? vì sao?
Cho 
Câu 4:(4 điểm)
Hình vẽ sau đây cho biết : a // b, 
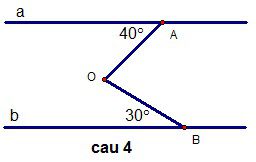
Tính 
4 tháng 10 2019
Ta có :
+, \(\frac{x}{4}=\frac{y}{3}\Leftrightarrow\frac{x}{8}=\frac{y}{6}\left(1\right)\)
+, \(\frac{y}{2}=\frac{z}{5}\Leftrightarrow\frac{y}{6}=\frac{z}{15}\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrow\frac{x}{8}=\frac{y}{6}=\frac{z}{15}\)
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{8}=\frac{y}{6}=\frac{z}{15}=\frac{x+y+z}{8+6+15}=\frac{5}{29}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{x}{8}=\frac{5}{29}\\\frac{y}{6}=\frac{5}{29}\\\frac{z}{15}=\frac{5}{29}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\frac{40}{29}\\x=\frac{30}{29}\\z=\frac{75}{29}\end{matrix}\right.\)
Vậy...
TG
4 tháng 10 2019
Theo đề ta có: \(\frac{x}{4}=\frac{y}{3};\frac{y}{2}=\frac{z}{5};x+y+z=5\)
Vì: \(\frac{x}{4}=\frac{y}{3}\Rightarrow\frac{x}{8}=\frac{y}{6}\) (1)
\(\frac{y}{2}=\frac{z}{5}\Rightarrow\frac{y}{6}=\frac{z}{15}\) (2)
Từ (1) và (2), ta suy ra:
\(\frac{x}{8}=\frac{y}{6}=\frac{z}{15}\)
Theo tính chất dãy tỉ sô bằng nhau ta có:
\(\frac{x}{8}=\frac{y}{6}=\frac{z}{15}\)\(=\frac{x+y+z}{8+6+15}=\frac{5}{29}\)
x/8 = 5/29 => x = 5/29 . 8 = 40/29
y/6 = 5/29 => y = 5/29 . 6 = 30/29
z/15 = 5/29 => z = 5/29 . 15 = 75/29
12 tháng 3 2017
Vì \(\left(x+2\right)^2\ge0\forall x;\left|y-\frac{1}{5}\right|\ge0\forall y\)
\(\Rightarrow\left(x+2\right)^2+\left|y-\frac{1}{5}\right|\ge0\forall x;y\)
\(\Rightarrow A=\left(x+2\right)^2+\left|y-\frac{1}{5}\right|-10\ge-10\forall x;y\)
Dấu "=" xảy ra <=> \(\left(x+2\right)^2=0;\left|y-\frac{1}{5}\right|=0\)
\(\Rightarrow x=-2;y=\frac{1}{5}\)
Vậy \(A_{min}=-10\) tại \(x=-2;y=\frac{1}{5}\)
lx
lx