K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 2 2021
1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
22 tháng 2 2021
a) Phương trình hoành độ giao điểm là:
\(x^2=\left(m+2\right)x-2m\)
\(\Leftrightarrow x^2-\left(m+2\right)x+2m=0\)
\(\Delta=\left(m+2\right)^2-8m=m^2+4m+4-8m=m^2-4m+4=\left(m-2\right)^2\)
Để (d) và (P) cắt nhau tại hai điểm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow\left(m-2\right)^2>0\)
mà \(\left(m-2\right)^2\ge0\)
nên \(m-2\ne0\)
hay \(m\ne2\)
Vậy: Để (d) và (P) cắt nhau tại hai điểm phân biệt thì \(m\ne2\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 8 2021
ĐKXĐ: \(x\ge0\)
\(\Leftrightarrow3\sqrt{x}=\left(2\sqrt{x}-1\right)\left(2\sqrt{x}+3\right)\)
\(\Leftrightarrow4x+\sqrt{x}-3=0\)
\(\Leftrightarrow4x+4\sqrt{x}-3\sqrt{x}-3=0\)
\(\Leftrightarrow4\sqrt{x}\left(\sqrt{x}+1\right)-3\left(\sqrt{x}+1\right)=0\)
\(\Leftrightarrow\left(4\sqrt{x}-3\right)\left(\sqrt{x}+1\right)=0\)
\(\Leftrightarrow4\sqrt{x}-3=0\)
\(\Leftrightarrow x=\dfrac{9}{16}\)
19 tháng 8 2021
Ta có: \(\dfrac{3\sqrt{x}}{2\sqrt{x}+3}=2\sqrt{x}-1\)
\(\Leftrightarrow\left(2\sqrt{x}-1\right)\left(2\sqrt{x}+3\right)=3\sqrt{x}\)
\(\Leftrightarrow4x+6\sqrt{x}-2\sqrt{x}-3-3\sqrt{x}=0\)
\(\Leftrightarrow4x+\sqrt{x}-3=0\)
\(\Leftrightarrow\left(\sqrt{x}+1\right)\left(4\sqrt{x}-3\right)=0\)
\(\Leftrightarrow4\sqrt{x}-3=0\)
hay \(x=\dfrac{9}{16}\)
4 tháng 11 2021
Bài 2:
a) \(\Leftrightarrow\left|x-3\right|=9\\ \Leftrightarrow\left[{}\begin{matrix}x-3=-3\\x-3=3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
b) ĐKXĐ: \(x\ge-5\)
\(\Leftrightarrow2\sqrt{x+5}+\sqrt{x+5}-\sqrt{x+5}=4\\ \Leftrightarrow2\sqrt{x+5}=4\\ \Leftrightarrow\sqrt{x+5}=2\\ \Leftrightarrow x+5=4\\ \Leftrightarrow x=1\left(tm\right)\)
c) ĐKXĐ: \(x\ge3\)
b) \(\Leftrightarrow x-3-2\sqrt{x-3}+1=1\\ \Leftrightarrow\left(\sqrt{x-3}+1\right)^2=1\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}+1=1\\\sqrt{x-3}+1=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\\sqrt{x-3}=-2\left(vôlí\right)\end{matrix}\right.\\ \Leftrightarrow x-3=0\\ \Leftrightarrow x=3\left(tm\right)\)
17 tháng 12 2022
\(=\dfrac{x-4-x+2\sqrt{x}-3-3\sqrt{3}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\sqrt{x}-3\sqrt{3}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
14 tháng 6 2023
a: góc ASB=1/2*180=90 độ=góc ABM
b: ON vuông góc AS
BS vuông góc SA
=>ON//BS
c: góc OIM+góc OBM=180 độ
=>OIMB nội tiếp
AH
Akai Haruma
Giáo viên
9 tháng 6 2021
Lời giải:
Theo hình minh họa thì:
Chiều cao tòa nhà $=\tan 35^0.30\approx 21$ (m)
AH
Akai Haruma
Giáo viên
11 tháng 7 2021
Chữ mờ quá. Bạn nên gõ đề bằng công thức toán để được hỗ trợ tốt hơn.
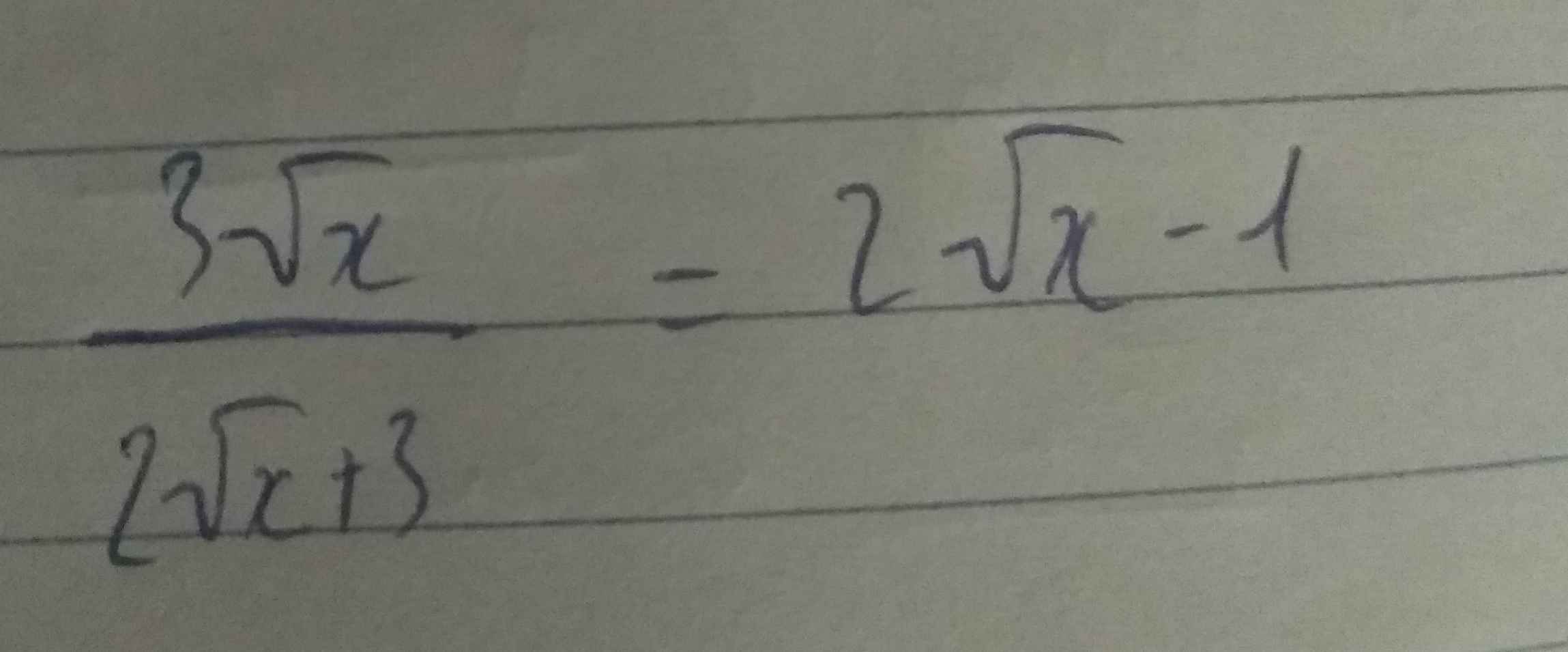
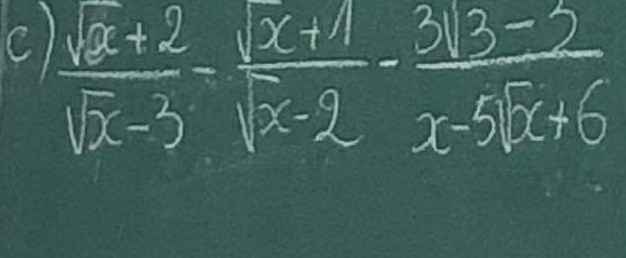
Bài 5.
\(P=\left(\frac{\sqrt{x}-2}{x-1}-\frac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\frac{\left(1-x\right)^2}{2}\)(đk: \(x\ge0,x\ne1\))
\(=\left[\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)}-\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)}\right].\frac{\left(x-1\right)^2}{2}\)
\(=\frac{x-\sqrt{x}-2-\left(x+\sqrt{x}-2\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)}.\frac{\left(x-1\right)^2}{2}\)
\(=\frac{-2\sqrt{x}}{\sqrt{x}+1}.\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{2}\)
\(=-\sqrt{x}\left(\sqrt{x}-1\right)=-x+\sqrt{x}\)
Nếu \(0< x< 1\)thì \(0< \sqrt{x}< 1\Rightarrow x< \sqrt{x}\Leftrightarrow\sqrt{x}-x>0\)
Suy ra \(P>0\).
\(P=-x+\sqrt{x}=-\left(x-\sqrt{x}+\frac{1}{4}\right)+\frac{1}{4}=-\left(\sqrt{x}-\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\)
Dấu \(=\)khi \(\sqrt{x}=\frac{1}{2}\Leftrightarrow x=\frac{1}{4}\).