
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


B, Đồ thị y thì nhìn vào dáng điệu, đồ thị y' thì chú ý trục hoành

dạ ko ạ,em hỏi mấy anh chị cho nhanh thôi ạ

`#3107.101107`
`A = 1+ 3 + 3^2+3^3+…+3^101?`
`= (1 + 3 + 3^2) + (3^3 + 3^4 + 3^5) + ... + (3^99 + 3^100 + 3^101)`
`= (1 + 3 + 3^2) + 3^3 * (1 + 3 + 3^2) + ... + 3^99 * (1 + 3 + 3^2)`
`= (1 + 3 + 3^2) * (1 + 3^3 + ... + 3^99)`
`= 13 * (1 + 3^3 + ... + 3^99)`
Vì `13 * (1 + 3^3 + ... + 3^99) \vdots 13`
`=> A \vdots 13`
Vậy, `A \vdots 13.`


\(A=log_m\left(8m\right)=log_mm+log_m8\)
\(=1+log_m8\)
\(=1+\dfrac{1}{log_8m}=1+\dfrac{1}{log_{2^3}m}=1+\dfrac{1}{\dfrac{1}{3}\cdot log_2m}\)
\(=1+\dfrac{1}{\dfrac{1}{3}a}=1+1:\dfrac{a}{3}=1+\dfrac{3}{a}=\dfrac{a+3}{a}\)
=>Chọn A

Cách làm nói chung:
- Tìm vecto chỉ phương \(\overrightarrow{u}\) của đường d và vtpt \(\overrightarrow{n}\) của mặt (P)
- Tính tích có hướng \(\overrightarrow{u_1}=\left(\overrightarrow{u};\overrightarrow{n}\right)\)
- Tiếp tục tính tích có hướng \(\overrightarrow{u_2}=\left[\overrightarrow{u_1};\overrightarrow{n}\right]\)
- Tìm tọa độ giao điểm M của d và (P)
- Hình chiếu vuông góc của d lên (P) sẽ đi qua M và nhận \(\overrightarrow{u_2}\) (hoặc 1 vecto cùng phương với nó) là 1 vtcp
Lưu ý rằng có vô số cách viết 1 pt đường thẳng (tùy thuộc cách chọn điểm) nên có thể trong 4 đáp án của đề bài không đáp án nào giống pt vừa viết được. Lúc đó cần kiểm tra bằng cách: 1. Loại những đáp án không giống vecto chỉ phương. 2. Trong những đáp án còn lại, tìm 1 điểm trên đó và thay vào pt đường thẳng vừa viết được, nếu thỏa mãn thì đó là đáp án đúng.
1209.
d nhận \(\overrightarrow{u}=\left(1;1;-1\right)\) là 1 vtcp
(P) nhận \(\overrightarrow{n}=\left(1;2;1\right)\) là 1 vtpt
Ta có: \(\overrightarrow{u_1}=\left[\overrightarrow{u};\overrightarrow{n}\right]=\left(3;-2;1\right)\)
\(\overrightarrow{u_2}=\left[\overrightarrow{u_1};\overrightarrow{n}\right]=\left(-4;-2;8\right)=-2\left(2;1;-4\right)\)
Phương trình d dạng tham số: \(\left\{{}\begin{matrix}x=t\\y=1+t\\z=2-t\end{matrix}\right.\)
Gọi M là giao điểm d và (P), tọa độ M thỏa mãn:
\(t+2\left(1+t\right)+2-t-4=0\Rightarrow t=0\Rightarrow M\left(0;1;2\right)\)
Do đó hình chiếu của d lên (P) nhận (2;1;-4) là 1 vtcp và đi qua M(0;1;2)
Phương trình: \(\dfrac{x}{2}=\dfrac{y-1}{1}=\dfrac{z-2}{-4}\)
Câu 1210 hoàn toàn tương tự

Gọi G là trọng tâm tam giác ABC
\(\overrightarrow{A'A}+\overrightarrow{B'B}+\overrightarrow{C'C}=\overrightarrow{0}\Leftrightarrow\overrightarrow{A'G}+\overrightarrow{GA}+\overrightarrow{B'G}+\overrightarrow{GB}+\overrightarrow{C'G}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=\overrightarrow{0}\)
Goi G la trong tam tam giac A'B'C'
Lai co: \(\overrightarrow{G'A'}+\overrightarrow{G'B'}+\overrightarrow{G'C'}=\overrightarrow{0}\)
\(\Rightarrow G'\equiv G\Rightarrow G'=\left(1;0;-2\right)\)

\(f\left(x\right)=ax^3+bx^2+cx+d\)
Dựa vào đồ thị ta có: \(f\left(-2\right)=2,f\left(-1\right)=-1,f\left(0\right)=0,f\left(1\right)=-1\)
Từ đó suy ra \(f\left(x\right)=-x^3-x^2+x\).
\(g\left(x\right)=\left|f^3\left(x\right)-3f\left(x\right)\right|\)
\(h\left(x\right)=f^3\left(x\right)-3f\left(x\right)\)
\(h'\left(x\right)=3f'\left(x\right)f^2\left(x\right)-3f'\left(x\right)\)
\(h'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f^2\left(x\right)=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f\left(x\right)=1\\f\left(x\right)=-1\end{matrix}\right.\)
\(f'\left(x\right)=0\) có \(2\) nghiệm đơn
\(f\left(x\right)=1\) có \(1\) nghiệm đơn
\(f\left(x\right)=-1\) có \(1\) nghiệm đơn, \(1\) nghiệm kép.
Kết hợp lại ta được phương trình \(h'\left(x\right)=0\) có \(4\) nghiệm bội lẻ (do nghiệm \(x=-1\) vừa là nghiệm kép của \(f\left(x\right)=-1\) vừa là nghiệm đơn của \(f'\left(x\right)=0\)).
mà \(limh\left(x\right)=-\infty\) do đó \(g\left(x\right)=\left|h\left(x\right)\right|\) có \(3\) điểm cực đại, \(4\) điểm cực tiểu suy ra \(T=n^m=4^3=64\).
Chọn A.


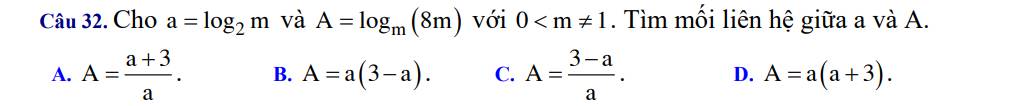



Phương trình hoành độ giao điểm của đường thẳng và đồ thị hàm số
Vậy đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt \(A\left(0;-2\right),B\left(-1,-3\right)\)
Đáp án : B