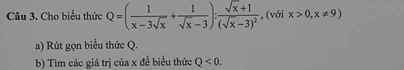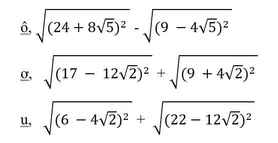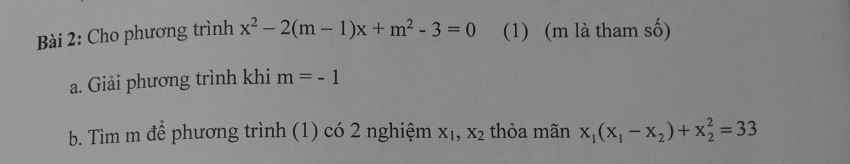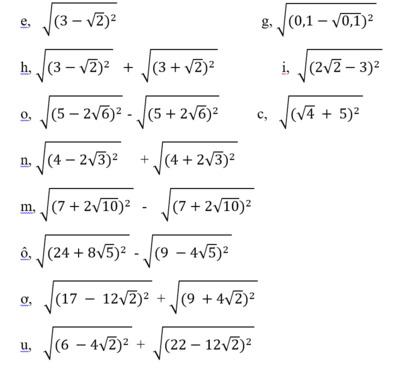K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NK
2
HN
22 tháng 7 2018
Bình phương 2 vế được
(x2 - 6x - 3)(x2 - 2x - 1) = 0
PS: Mấy cái điều kiện thì tự làm nha
22 tháng 7 2018
điều kiện \(x\ge\dfrac{-1}{2}\)
ta có : \(x^2-3x-2=\left(x-1\right)\sqrt{2x+1}\)
\(\Leftrightarrow\left(x^2-3x-2\right)^2=\left(x^2-2x+1\right)\left(2x+1\right)\)
\(\Leftrightarrow x^4+9x^2+4-6x^3+12x-4x^2=2x^3+x^2-4x^2-2x+2x+1\)
\(\Leftrightarrow x^4-8x^3+8x^2+12x+3=0\)
\(\Leftrightarrow x^4-2x^3-x^2-6x^3+12x^2+6x-3x^2+6x+3=0\)
\(\Leftrightarrow x^2\left(x^2-2x-1\right)-6x\left(x^2-2x-1\right)-3\left(x^2-2x-1\right)=0\)
\(\Leftrightarrow\left(x^2-2x-1\right)\left(x^2-6x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1-\sqrt{2}\\x=1+\sqrt{2}\\x=3+2\sqrt{3}\\x=3-2\sqrt{3}\end{matrix}\right.\) nhận hết .
vậy ......................................................................................................................
TD
12 tháng 2 2022
a) Với x>0,x\(\ne\)9
\(Q=\left(\dfrac{1}{x-3\sqrt{x}}+\dfrac{1}{\sqrt{x}-3}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-3\right)^2}=\left(\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-3\right)}\right).\dfrac{\left(\sqrt{x}-3\right)^2}{\sqrt{x}+1}=\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
b)Với x>0,x\(\ne\)9
\(Q< 0< =>\dfrac{\sqrt{x}-3}{\sqrt{x}}< 0\)
\(< =>\sqrt{x}-3< 0\left(Vì\sqrt{x}>0\right)\)
\(< =>\sqrt{x}< 3\)
\(< =>x< 9\)
Kết hợp với ĐKXĐ ta được
0<x<9
5 tháng 2 2022
\(\sqrt{\left(24+8\sqrt{5}\right)^2}-\sqrt{\left(9-4\sqrt{5}\right)^2}=24+8\sqrt{5}-9+4\sqrt{5}=15+12\sqrt{5}\)
\(\sqrt{\left(17-12\sqrt{2}\right)^2}+\sqrt{\left(9+4\sqrt{2}\right)^2}=17-12\sqrt{2}+9+4\sqrt{2}=26-8\sqrt{2}\)
\(\sqrt{\left(6-4\sqrt{2}\right)^2}+\sqrt{\left(22-12\sqrt{2}\right)^2}=6-4\sqrt{2}+22-12\sqrt{2}=28-16\sqrt{2}\)
5 tháng 2 2022
\(ô,\\ \Rightarrow24+8\sqrt{5}-\sqrt{\left(9-4\sqrt{5}\right)^2}\\ \Rightarrow24+8\sqrt{5}-\left(9-4-\sqrt{5}\right)\\ \Rightarrow24+8\sqrt{5}-9+4\sqrt{5}\\ \Rightarrow15+8\sqrt{5}+4\sqrt{5}\\ \Rightarrow15+12\sqrt{5}\)
\(ơ,\\ g\left(17-12\sqrt{2}\right)+\sqrt{\left(9+4\sqrt{2}\right)^2}\\ \Rightarrow g\left(17-12\sqrt{2}\right)+\sqrt{\left(9+4+\sqrt{2}\right)^2}\\ \Rightarrow\left(17-12\sqrt{2}\right)g+\sqrt{\left(9+4\sqrt{2}\right)^2}\\ \Rightarrow\left(17-12\sqrt{2}\right)g+9+4\sqrt{2}\)
\(u,\\ 6-4\sqrt{2}+\sqrt{\left(22-12\sqrt{2}\right)}^2\\ \Rightarrow6-4\sqrt{2}+22-12\sqrt{2}\\ \Rightarrow28-4\sqrt{2}-12\sqrt{2}\\ \Rightarrow28-16\sqrt{2}\)
2
19 tháng 5 2023
Ptr hoành độ của `(P)` và `(d)` là:
`x^2=-5x-3m+1`
`<=>x^2+5x+3m-1=0` `(1)`
Để `(P)` cắt `(d)` tại `2` điểm phân biệt thì ptr `(1)` có `2` nghiệm phân biệt
`=>\Delta > 0`
`<=>5^2-4(3m-1) > 0`
`<=>25-12m+4 > 0`
`<=>m < 29/12`
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=-5),(x_1.x_2=c/a=3m-1):}`
Ta có: `[x_1 ^2]/[x_2]-[x_2 ^2]/[x_1]+3=75/[x_1.x_2]`
`<=>[x_1 ^3-x_2 ^3]/[x_1.x_2]+[3x_1.x_2]/[x_1.x_2]=75/[x_1.x_2]`
`=>(x_1-x_2)(x_1 ^2+x_1.x_2+x_2 ^2)+3x_1.x_2=75`
`<=>(x_1-x_2)[(x_1+x_2)^2-x_1.x_2]+3x_1.x_2=75`
`<=>(x_1-x_2)[(-5)^2-3m+1]+3(3m-1)=75`
`<=>(x_1-x_2)(26-3m)=78-9m`
`<=>x_1-x_2=[3(26-3m)]/[26-3m]`
`<=>x_1-x_2=3`
Kết hợp với `x_1+x_2=-5`
Giải hệ `=>{(x_1=-1),(x_2=-4):}`
Thay vào `x_1.x_2=3m-1` có:
`-1.(-4)=3m-1`
`<=>m=5/3` (t/m)
16 tháng 12 2023
a: Ta có: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD
Xét tứ giác OCBD có
H là trung điểm chung của OB và CD
=>OCBD là hình bình hành
Hình bình hành OCBD có OC=OD
nên OCBD là hình thoi
b: Xét ΔOCM vuông tại C có CH là đường cao
nên \(OH\cdot OM=OC^2\)
=>\(OH\cdot OM=OC\cdot OC\)
c: Ta có: ΔOCD cân tại O
mà OM là đường cao
nên OM là phân giác của góc COD
Xét ΔCOM và ΔDOM có
OC=OD
\(\widehat{COM}=\widehat{DOM}\)
OM chung
Do đó: ΔCOM=ΔDOM
=>\(\widehat{OCM}=\widehat{ODM}\)
mà \(\widehat{OCM}=90^0\)
nên \(\widehat{ODM}=90^0\)
=>DM\(\perp\)OD
Ta có: OCBD là hình thoi
=>OD//BC
Ta có: BC//OD
OD\(\perp\)DM
Do đó; CB\(\perp\)DM
Xét (I) có
ΔBEM nội tiếp
BM là đường kính
Do đó: ΔBEM vuông tại E
=>BE\(\perp\)EM tại E
=>BE\(\perp\)CM tại E
Xét ΔCDM có
CB,MH là các đường cao
CB cắt MH tại B
Do đó: B là trực tâm của ΔCDM
=>DB\(\perp\)CM
mà BE\(\perp\)CM
và DB,BE có điểm chung là B
nên D,B,E thẳng hàng
OCBD là hình thoi
=>BC=BD
=>ΔBCD cân tại B
=>\(\widehat{BCD}=\widehat{BDC}\)
Ta có: OCBD là hình thoi
=>BO là phân giác của góc CBD
=>\(\widehat{CBO}=\widehat{DBO}\)
Ta có: IB=IE
=>ΔIBE cân tại I
=>\(\widehat{IBE}=\widehat{IEB}\)
mà \(\widehat{IBE}=\widehat{HBD}\)(hai góc đối đỉnh)
nên \(\widehat{IEB}=\widehat{HBD}\)
=>\(\widehat{IEB}=\widehat{CBO}\)
Xét tứ giác CHBE có \(\widehat{CHB}+\widehat{CEB}=90^0+90^0=180^0\)
nên CHBE là tứ giác nội tiếp
=>\(\widehat{HCB}=\widehat{HEB}\)
Ta có: \(\widehat{IEH}=\widehat{IEB}+\widehat{HEB}\)
\(=\widehat{HCB}+\widehat{CBH}=90^0\)
=>HE là tiếp tuyến của (I)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 3 2022
a.
Với \(m=-1\) pt trở thành: \(x^2+4x-2=0\)
\(\Delta'=4+2=6>0\) nên pt có 2 nghiệm pb:
\(x_1=-2+\sqrt{6}\) ; \(x_2=-2-\sqrt{6}\)
b.
\(\Delta'=\left(m-1\right)^2-\left(m^2-3\right)=-2m+4\ge0\Rightarrow m\le2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3\end{matrix}\right.\)
\(x_1\left(x_1-x_2\right)+x_2^2=33\)
\(\Leftrightarrow x_1^2+x_2^2-x_1x_2=33\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=33\)
\(\Leftrightarrow4\left(m-1\right)^2-3\left(m^2-3\right)=33\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10>2\left(loại\right)\\m=-2\end{matrix}\right.\)
12 tháng 4 2022
a: Thay x=2 và y=0 vào (d), ta được:
-n+3+4=0
=>1-n=0
hay n=1
b: Phương trình hoành độ giao điểm là:
\(x^2-2x+n-3=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot\left(n-3\right)=-4n+12+4=-4n+16\)
Để phương trình có hai nghiệm phân biệt thì -4n+16>0
hay n<4
HK
1
4 tháng 2 2022
e: \(=\left|3-\sqrt{2}\right|=3-\sqrt{2}\)
h: \(=3-\sqrt{2}+3+\sqrt{2}=6\)
g: \(=\left|0.1-\sqrt{0.1}\right|=0.1-\sqrt{0.1}\)
i: \(=\left|2\sqrt{2}-3\right|=3-2\sqrt{2}\)
c: \(=\left|2+5\right|=7\)
o: \(=5-2\sqrt{6}-5-2\sqrt{6}=-4\sqrt{6}\)
n: \(=4-2\sqrt{3}+4+2\sqrt{3}=8\)
m: \(=7+2\sqrt{10}-7-2\sqrt{10}=0\)
HK
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 3 2022
a.
Với \(m=3\) pt trở thành: \(2x^2+5x+2=0\)
\(\Delta=5^2-4.2.2=9>0\) nên pt có 2 nghiệm phân biệt:
\(x_1=\dfrac{-5+\sqrt{9}}{2.2}=-\dfrac{1}{2}\)
\(x_2=\dfrac{-5-\sqrt{9}}{2.2}=-2\)
b.
\(\Delta=\left(2m-1\right)^2-8\left(m-1\right)=4m^2-12m+9=\left(2m-3\right)^2\ge0;\forall m\)
Phương trình luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{2m-1}{2}\\x_1x_2=\dfrac{m-1}{2}\end{matrix}\right.\)
\(4x_1^2+2x_1x_2+4x_2^2=1\)
\(\Leftrightarrow4\left(x_1^2+2x_1x_2+x_2^2\right)-6x_1x_2=1\)
\(\Leftrightarrow4\left(x_1+x_2\right)^2-6x_1x_2=1\)
\(\Leftrightarrow\left(2m-1\right)^2-3\left(m-1\right)=1\)
\(\Leftrightarrow4m^2-7m+3=0\Rightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{3}{4}\end{matrix}\right.\)