K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 9 2021
Tất cả \(k\in Z\)
1.
a. \(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k2\pi\)
Đáp án trong đề bị sai
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 9 2021
b.
\(\Leftrightarrow\dfrac{1}{2}cos7x-\dfrac{\sqrt{3}}{2}sin7x=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow cos\left(7x+\dfrac{\pi}{3}\right)=cos\left(\dfrac{3\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}7x+\dfrac{\pi}{3}=\dfrac{3\pi}{4}+k2\pi\\7x+\dfrac{\pi}{3}=-\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}7x=\dfrac{5\pi}{12}+k2\pi\\7x=-\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{84}+\dfrac{k2\pi}{7}\\x=-\dfrac{13\pi}{84}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
Do \(\dfrac{2\pi}{5}\le x\le\dfrac{6\pi}{7}\Rightarrow\left[{}\begin{matrix}\dfrac{2\pi}{5}\le\dfrac{5\pi}{84}+\dfrac{k2\pi}{7}\le\dfrac{6\pi}{7}\\\dfrac{2\pi}{5}\le-\dfrac{13\pi}{84}+\dfrac{k2\pi}{7}\le\dfrac{6\pi}{7}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{143}{120}\le k\le\dfrac{67}{24}\\\dfrac{233}{120}\le k\le\dfrac{85}{24}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}k=1\\k=\left\{2;3\right\}\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{53\pi}{84};\dfrac{5\pi}{12};\dfrac{59\pi}{84}\right\}\)
HP
8 tháng 9 2021
1.
c, \(sin\left(\dfrac{\pi}{3}-x\right)=-\dfrac{1}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{3}-x=arcsin\left(-\dfrac{1}{4}\right)+k.360^o\\\dfrac{\pi}{3}-x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k.360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}-arcsin\left(-\dfrac{1}{4}\right)+k.360^o\\x=-\dfrac{2\pi}{3}+arcsin\left(-\dfrac{1}{4}\right)+k.360^o\end{matrix}\right.\)
d, \(sin4x=\dfrac{2}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=arcsin\dfrac{2}{3}+k2\pi\\4x=\pi-arcsin\dfrac{2}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}arcsin\dfrac{2}{3}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{4}-\dfrac{1}{4}arcsin\dfrac{2}{3}+\dfrac{k\pi}{2}\end{matrix}\right.\)
HP
8 tháng 9 2021
1.
e, \(2sin2x+\sqrt{2}=0\)
\(\Leftrightarrow sin2x=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin2x=sin\left(-\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-\dfrac{\pi}{4}+k2\pi\\2x=\dfrac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{8}+k\pi\\x=\dfrac{5\pi}{8}+k\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
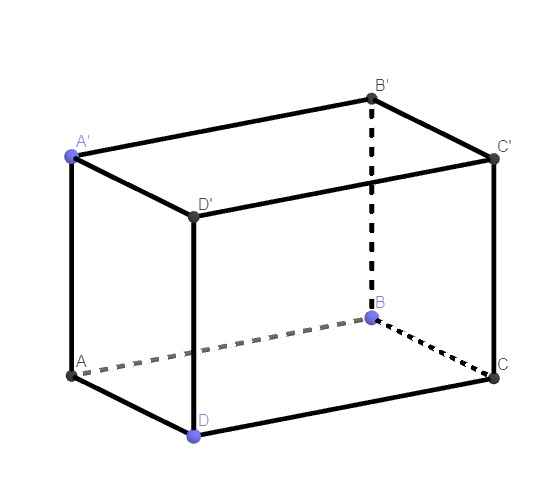
71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)
PT
2
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
2.
\(cos\left(x-5\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow cos\left(x-5\right)=cos\left(\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=\dfrac{\pi}{6}+k2\pi\\x-5=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=5+\dfrac{\pi}{6}+k2\pi\\x=5-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{5-\dfrac{11\pi}{6};5-\dfrac{13\pi}{6}\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
4.
\(\Leftrightarrow cot3x=cot\left(-\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow3x=-\dfrac{\pi}{3}+k\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{9}+\dfrac{k\pi}{3}\)
\(-\dfrac{\pi}{2}< x< 0\Rightarrow-\dfrac{\pi}{2}< -\dfrac{\pi}{9}+\dfrac{k\pi}{3}< 0\)
\(\Rightarrow-\dfrac{7}{6}< k< \dfrac{1}{3}\)
\(\Rightarrow k=\left\{-1;0\right\}\)
\(\Rightarrow x=\left\{-\dfrac{4\pi}{9};-\dfrac{\pi}{9}\right\}\)
NT
1
NT
6
17 tháng 10 2021
a) \(\left(2m-1\right)sinx+1-m=0\Rightarrow sinx=\dfrac{m-1}{2m-1}\)
Pt có nghiệm: \(-1\le\dfrac{m-1}{2m-1}\le1\)
\(\Rightarrow1-2m\le m-1\le2m-1\Rightarrow m\ge\dfrac{2}{3}\)
17 tháng 10 2021
b) \(\left(m+1\right)sin3x-cos3x=m+2\)
Pt có nghiệm: \(\left(m+1\right)^2+\left(-1\right)^2\ge\left(m+2\right)^2\)
\(\Rightarrow m^2+2m+1+1\ge m^2+4m+4\)
\(\Rightarrow-2m\ge2\Rightarrow m\le-1\)
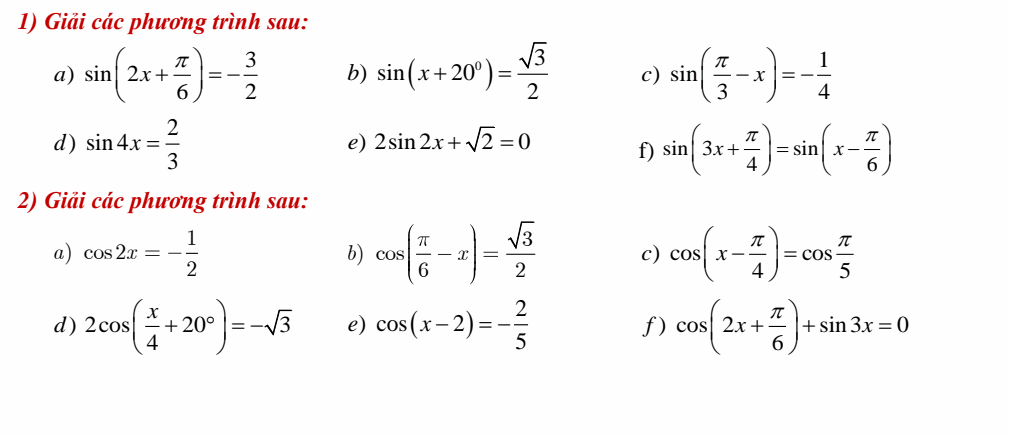
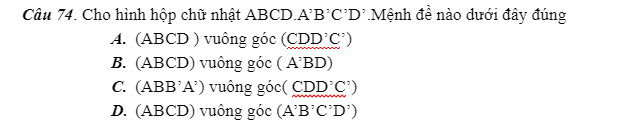
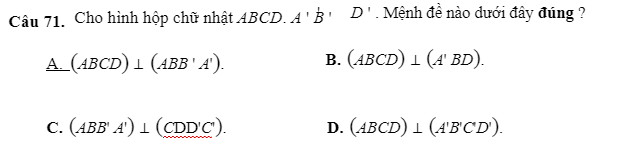
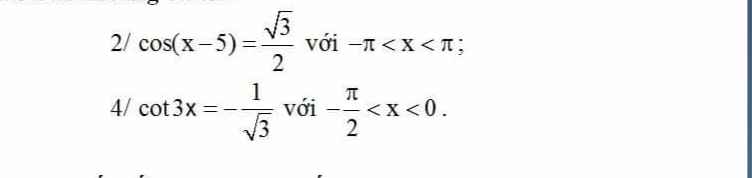
1A 2B 20A 19C 18A
17B 16A 15C 13D 12D