Question

[Mot So]

giải giúp mình với :)

Answer 1

[Nguyễn Lê Phước Thịnh]

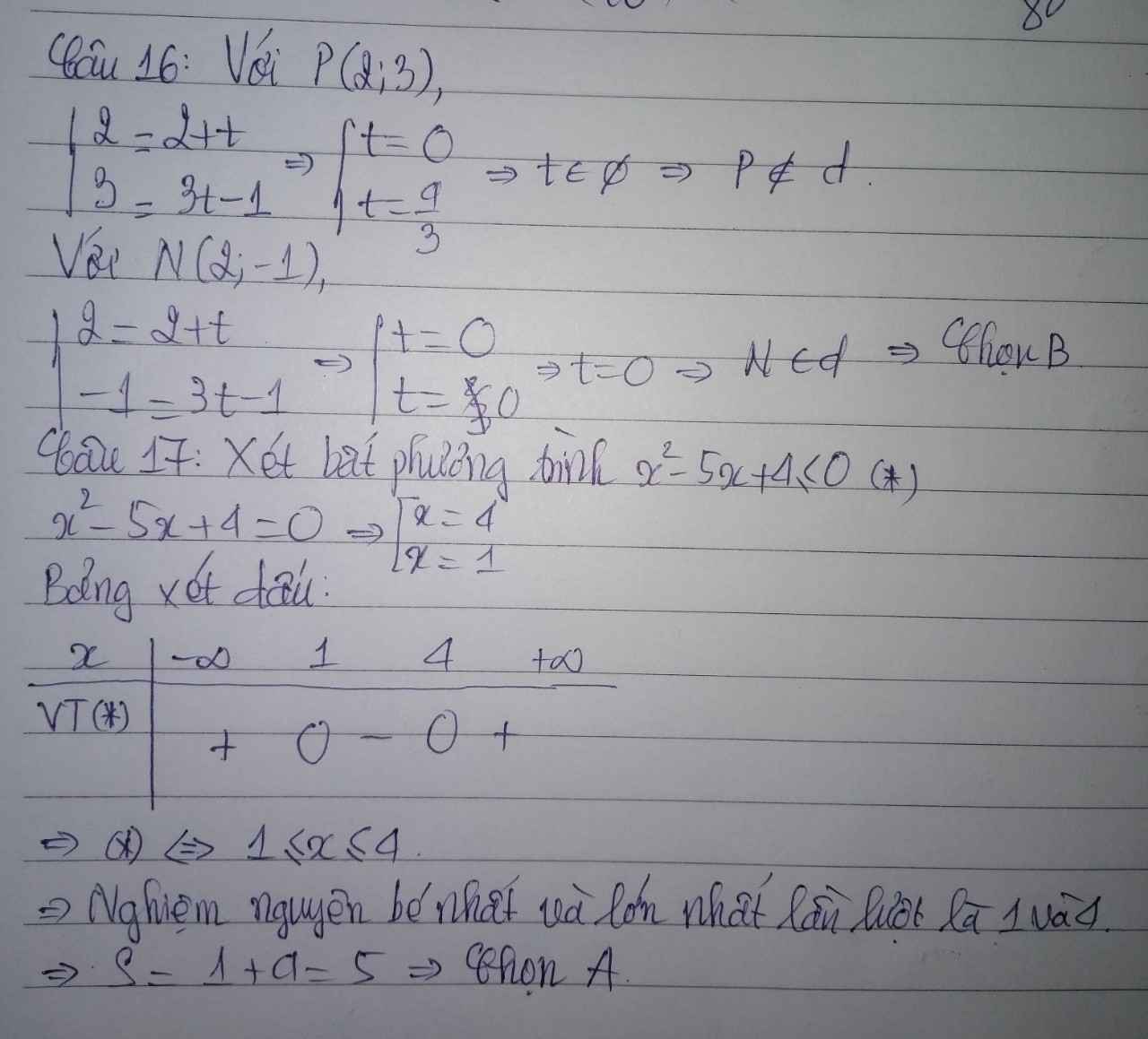
a: Tọa độ điểm M là:

\(\left\{{}\begin{matrix}x=\dfrac{6+12}{2}=\dfrac{18}{2}=9\\y=\dfrac{-2+4}{2}=\dfrac{2}{2}=1\end{matrix}\right.\)

Ta có: A(2;4); M(9;1)

\(\Leftrightarrow\overrightarrow{AM}=\left(8;-3\right)\)

Phương trình tham số của đường thẳng AM là:

\(\left\{{}\begin{matrix}x=2+8t\\y=4-3t\end{matrix}\right.\)

\(\overrightarrow{BC}=\left(6;6\right)=\left(1;1\right)\)

Vì AH\(\perp\)BC nên AH nhận \(\overrightarrow{BC}\) làm vecto pháp tuyến

=>VTPT của phương trình tổng quát của đường cao AH là (1;1)

Phương trình tổng quát của đường cao AH là:

1(x-2)+1(y-4)=0

=>x-2+y-4=0

=>x+y-6=0

b: \(\overrightarrow{BC}=\left(1;1\right)\)

=>VTPT là (-1;1)

Phương trình đường thẳng BC là:

-1(x-6)+1(y+2)=0

=>-x+6+y+2=0

=>-x+y+8=0

BC: -x+y+8=0

AH: x+y-6=0

Tọa độ điểm H là:

\(\left\{{}\begin{matrix}-x+y+8=0\\x+y-6=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-x+y=-8\\x+y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2y=-2\\x+y=6\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=-1\\x=6-y=6-\left(-1\right)=7\end{matrix}\right.\)

Vậy: H(7;-1)