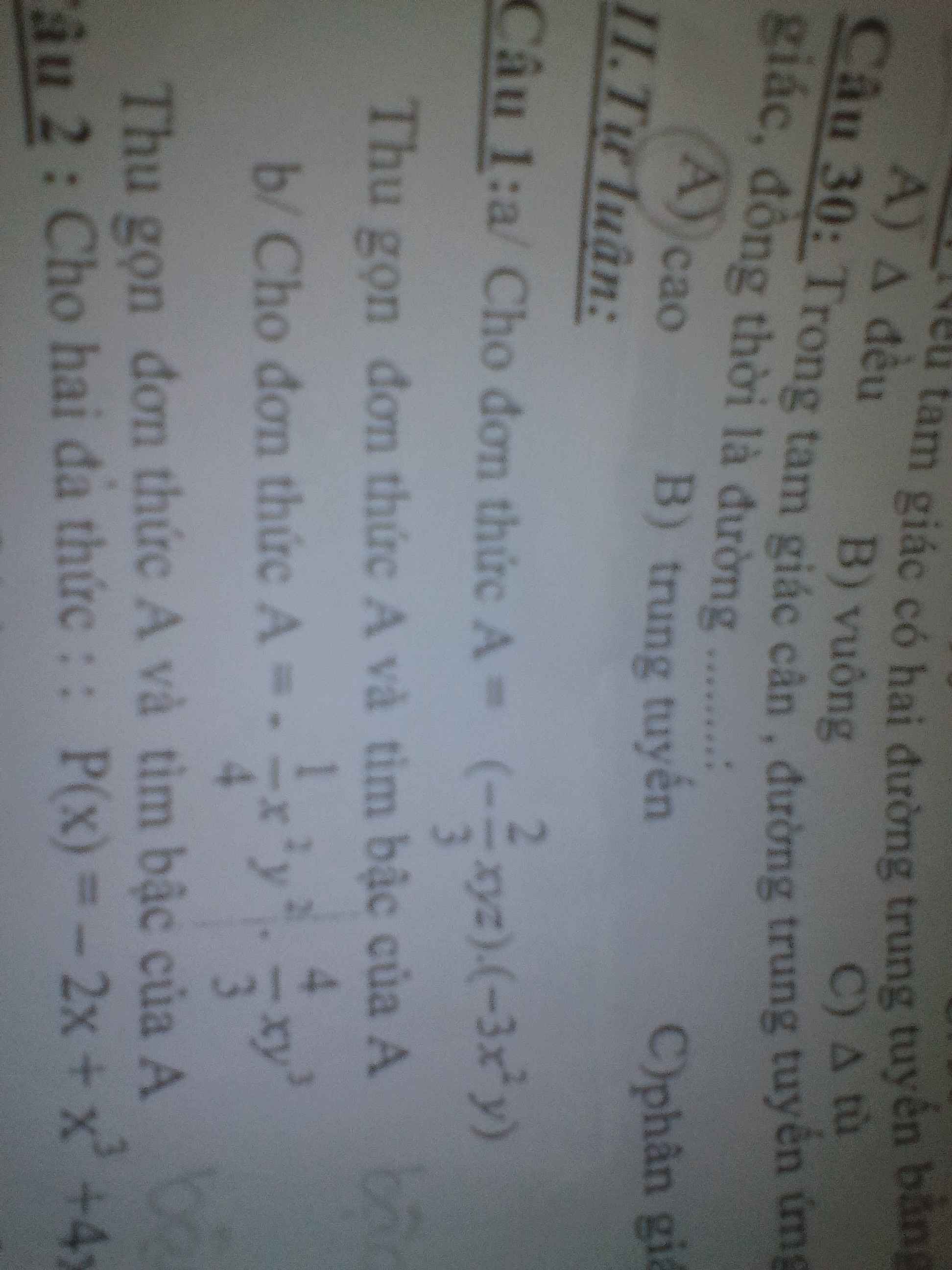K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 5 2021
a) [\(\dfrac{-2}{3}\).(-3)]. (x.x^2).(y.y).z
=2x^3y^2z
- Bậc: 6
b) A=\(\dfrac{-1}{4}\)x^2y^2. \(\dfrac{4}{3}\)xy^3
= (\(\dfrac{-1}{4}\) . \(\dfrac{4}{3}\)). ( x^2.x). ( y^2.y^3)
= \(\dfrac{-1}{3}\)x^3y^5
- Bậc: 8
CK
1
7 tháng 5 2022
\(f(x)=ax^2+bx+6\)
Để \(f(x)\) là đa thức bậc \(1\) thì \(ax^2=0\)
\(→a=0\)
Thay \(x=1\) vào \(f(x)=ax^2+bx+6\)
\(f(1)=b.1+6=b+6\)
Mà \(f(1)=3\)
\(\Rightarrow b+6=3\Rightarrow b=3−6\Rightarrow b=−3\)
Vậy \(a=0;b=−3\)
28 tháng 12 2020
a) Xét ΔABM và ΔACM có
AB=AC(gt)
AM chung
BM=CM(M là trung điểm của BC)
Do đó: ΔABM=ΔACM(c-c-c)
⇒\(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
mà tia AM nằm giữa hai tia AB,AC
nên AM là tia phân giác của \(\widehat{BAC}\)(đpcm)
b) Xét ΔCBN và ΔCDN có
CB=CD(gt)
\(\widehat{BCN}=\widehat{DCN}\)(CN là tia phân giác của \(\widehat{BCD}\))
CN chung
Do đó: ΔCBN=ΔCDN(c-g-c)
⇒\(\widehat{CNB}=\widehat{CND}\)(hai góc tương ứng)
mà \(\widehat{CNB}+\widehat{CND}=180^0\)(hai góc kề bù)
nên \(\widehat{CNB}=\widehat{CND}=\dfrac{180^0}{2}=90^0\)
hay CN⊥BD(đpcm)
c) Ta có: AB=AC(gt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MB=MC(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của BC
hay AM⊥BC
Xét ΔABM vuông tại M có
\(\widehat{ABM}+\widehat{BAM}=90^0\)(hai góc nhọn phụ nhau)(3)
Xét ΔBCN vuông tại N có
\(\widehat{NBC}+\widehat{BCN}=90^0\)(hai góc nhọn phụ nhau)(4)
Từ (3) và (4) suy ra \(\widehat{BAM}=\widehat{BCN}\)
mà \(\widehat{BAM}=\dfrac{1}{2}\cdot\widehat{BAC}\)(AM là tia phân giác của \(\widehat{BAC}\))
và \(\widehat{BCN}=\dfrac{1}{2}\cdot\widehat{DCB}\)(CN là tia phân giác của \(\widehat{DCB}\))
nên \(\widehat{BAC}=\widehat{DCB}\)(5)
Xét ΔABC có \(\widehat{ECB}\) là góc ngoài tại đỉnh C
nên \(\widehat{ECB}=\widehat{ABC}+\widehat{BAC}\)(Định lí góc ngoài của tam giác)(6)
Xét ΔBDC có \(\widehat{ADC}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADC}=\widehat{DBC}+\widehat{DCB}\)(Định lí góc ngoài của tam giác)
hay \(\widehat{ADC}=\widehat{ABC}+\widehat{DCB}\)(7)
Từ (5), (6) và (7) suy ra \(\widehat{ECB}=\widehat{ADC}\)
Xét ΔBCE và ΔCDA có
BC=CD(gt)
\(\widehat{ECB}=\widehat{ADC}\)(cmt)
CE=DA(gt)
Do đó: ΔBCE=ΔCDA(c-g-c)
⇒BE=CA(hai cạnh tương ứng)
mà BA=CA(gt)
nên BA=BE(đpcm)
NH
1
12 tháng 8 2023
`@` `\text {Ans}`
`\downarrow`
`c)`
\(2-3^{x-1}-7=11\)
`\Rightarrow`\(3^{x-1}-5=11\)
`\Rightarrow`\(3^{x-1}=11+5\)
`\Rightarrow`\(3^{x-1}=16\)
Bạn xem lại đề
`d)`
\(\left(x-\dfrac{3}{5}\right)\div\dfrac{-1}{3}=-0,4\)
`\Rightarrow`\(x-\dfrac{3}{5}=-0,4\cdot\left(-\dfrac{1}{3}\right)\)
`\Rightarrow`\(x-\dfrac{3}{5}=\dfrac{2}{15}\)
`\Rightarrow`\(x=\dfrac{2}{15}+\dfrac{3}{5}\)
`\Rightarrow`\(x=\dfrac{11}{15}\)
Vậy, \(x=\dfrac{11}{15}\)
29 tháng 7 2023
1:
a: A=x^4+6x^3-3x^2-4x+8
bậc là 4
B=-x^4-6x^3+3x^2-2x+5
bậc là 4
b: A(x)+B(x)
=x^4+6x^3-3x^2-4x+8-x^4-6x^3+3x^2-2x+5
=-6x+13
A(x)-B(x)
=x^4+6x^3-3x^2-4x+8+x^4+6x^3-3x^2+2x-5
=2x^4+12x^3-6x^2-2x+3
PT
1
5 tháng 11 2021
\(=\dfrac{2^{15}\cdot3^8}{3^6\cdot2^6\cdot2^9}+\dfrac{9^3\cdot71}{3^2\cdot71}=3^2+81=90\)
5 tháng 11 2021
\(=\dfrac{2^4\cdot5^4\cdot3^6}{2^8\cdot3^4}=3^2\cdot5^4\cdot\dfrac{1}{2^4}\)