
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(sin 2x-(2sin^2 x-sin2x-2sinx-1/2.\sin 2x+\cos^2x+\cos x-3\sin x-3\cos x+3)=0\)
\(5\sin x.\cos x+5\sin x+2\cos x-\sin^2x-4=0\)
\(\cos x(5\sin x+2)=\sin^2x-5\sin x+4=(\sin x-1)(\sin x -4)\)
Bình phương 2 vế suy ra
\((1-\sin^2 x)(5\sin x+2)^2=(1-\sin x)^2(\sin x-4)^2\)
TH1: \(\sin x=1\)
TH 2: \((1+\sin x)(5\sin x+2)^2=(1-\sin x)(\sin x-4)^2\)

Ví dụ 10^2 là 100 ( 2 chữ số 0 ) ; 10^3 có 1000 ( 3 chữ số 0) => số chữ số 0 tương ứng với số mũ => 10^303 có 303 số 0 :3

Trả lời :
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
= (1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 10 + 5
= 10 + 10 + 10 + 10 + 10 + 5
= 55

ý a,b,c cho 2 tung độ bằng nhau => tính được x1, x2 rồi áp dụng CT diện tích như thường
ý d cũng vậy => tính được x1, x2 nhưng phải xét điều kiện của e^x (x>0)
ý e :
ta có y' = 2x-2 mà M thuộc y' => y' = 4
=> PTTT là: y= 4x-7
xét x^2-2x+2 = 4x-7
=> tính được x1, x2 rồi áp dụng công thức diện tích như 4 ý trên

a/ \(\left(P\right):3\left(x-0\right)+0\left(y-2\right)+1\left(z+5\right)=0\Rightarrow\left(P\right):3x+z+5=0\)
b/\(\overrightarrow{AB}\left(2;4;-9\right);\overrightarrow{AC}\left(4;0;-7\right)\)
\(\overrightarrow{n_{\left(P\right)}}=\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(4.\left(-7\right)-0.\left(-9\right);\left(-9\right).4-\left(-7\right).2;2.0-4.4\right)=\left(-28;-22;-16\right)\)
\(\Rightarrow\left(P\right):-28\left(x-0\right)-22\left(y-1\right)-16\left(z-7\right)=0\Rightarrow\left(P\right):28x+22y+16z-134=0\)
c/ Truc Oy di qua O(0;0;0) va co vtcp \(\overrightarrow{j}\left(0;1;0\right)\)
\(\overrightarrow{OD}\left(3;-6;2\right)\)
\(\Rightarrow\overrightarrow{n_{\left(P\right)}}=\left[\overrightarrow{j};\overrightarrow{OD}\right]=\left(2;0;-3\right)\)
\(\Rightarrow\left(P\right):2\left(x-0\right)+0\left(y-1\right)-3\left(z-0\right)=0\Rightarrow\left(P\right):2x-3z=0\)
d/ \(\overrightarrow{Oz}\left(0;0;1\right)\)
\(\overrightarrow{DE}\left(5;-2;-7\right)\)
\(\Rightarrow\overrightarrow{n_{\left(P\right)}}=\left[\overrightarrow{Oz};\overrightarrow{DE}\right]=\left(2;5;0\right)\)
\(\Rightarrow\left(P\right):2\left(x-0\right)+5\left(y-0\right)+0\left(z-1\right)=0\Rightarrow\left(P\right):2x+5y=0\)
e/ \(\overrightarrow{n_{Oyz}}=\overrightarrow{n_{\left(P\right)}}=\left(1;0;0\right)\)
\(\Rightarrow\left(P\right):1\left(x-3\right)=0\Rightarrow\left(P\right):x-3=0\)
f/ Cách làm giống câu b
g/ \(\overrightarrow{HI}=\overrightarrow{IK}\Rightarrow\left\{{}\begin{matrix}x_I=\dfrac{3-1}{2}=1\\y_I=\dfrac{-1+5}{2}=2\\z_1=\dfrac{2-4}{2}=-1\end{matrix}\right.\Rightarrow I\left(1;2;-1\right)\)
\(\overrightarrow{n_{\left(P\right)}}=\overrightarrow{HK}\left(-4;6;-6\right)\)
\(\Rightarrow\left(P\right):-4\left(x-1\right)+6\left(y-2\right)-6\left(z+1\right)=0\Rightarrow\left(P\right):-4x+6y-6z+2=0\)
P/s: Bạn tính toán lại kết quả hộ mình nhé !

TXĐ: D=R, y'=-x2+10x-26=0 < 0 với mọi x.
Vậy hàm số đã cho nghịch biến trên khoảng (-\(\infty\);+\(\infty\)).

Vì tam giác \(ABC\)vuông cân tại \(A\)nên \(\frac{BC}{AB}=\sqrt{2}\).
Suy ra \(\frac{PC}{PB}=\frac{PB}{PA}=\frac{BC}{AB}=\sqrt{2}\)
\(\Rightarrow\Delta PBC\)đồng dạng với \(\Delta PAB\).
\(\Rightarrow\widehat{PBC}=\widehat{PAB}\)
\(\widehat{APB}=180^o-\widehat{PAB}-\widehat{PBA}=180^o-\widehat{PBC}-\widehat{PBA}=180^o-\widehat{ABC}=135^o\)
Dạng toán về tam giác đồng dạng nên có thể là nằm toán 8 nha bạn.


goi \(z=a+bi\)
\(\Rightarrow\)\(\left|z\right|+z=3+4i\Leftrightarrow\sqrt{a^2+b^2}+a+bi=3+4i\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{a^2+b^2}+a=3\\b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}3-a\ge0\\a^2+b^2=\left(3-a\right)^2\end{matrix}\right.\\b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-7}{6}\\b=4\end{matrix}\right.\Rightarrow z=\dfrac{-7}{6}+4i\)
 giup minh voi
giup minh voi giup mình voi ạ
giup mình voi ạ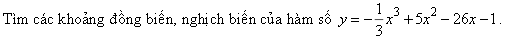
 Ai Giai Dung Chinh Xac Cach Lam Va Ket Qua Dau Tien Mik Cham Cho
Ai Giai Dung Chinh Xac Cach Lam Va Ket Qua Dau Tien Mik Cham Cho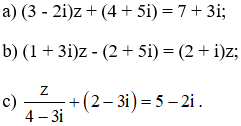
er là j bn?
ho mik di cac ban oi!