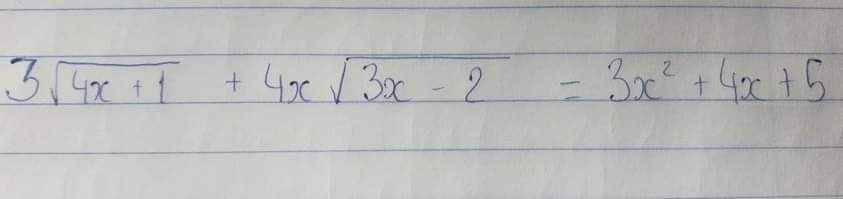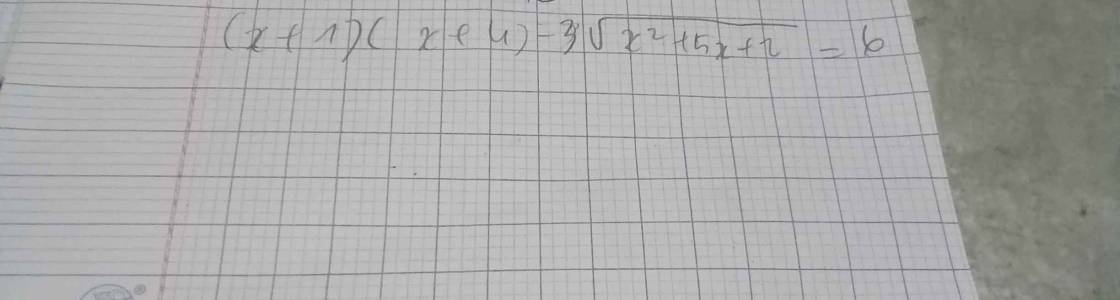K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 7 2023
1.4:
a: CH=16^2/24=256/24=32/3
BC=24+32/3=104/3
AC=căn 32/3*104/3=16/3*căn 13
b: BC=12^2/6=24
AC=căn 24^2-12^2=12*căn 3
CH=24-6=18
DH
1
24 tháng 9 2021
\(\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{AC}{AB}=\tan\alpha\)
\(\dfrac{\cos\alpha}{\sin\alpha}=\dfrac{AB}{BC}:\dfrac{AC}{BC}=\dfrac{AB}{AC}=\cot\alpha\)
\(\tan\alpha\cot\alpha=\dfrac{AC}{AB}\cdot\dfrac{AB}{AC}=1\)
\(\sin^2\alpha+\cos^2\alpha=\dfrac{AC^2}{BC^2}+\dfrac{AB^2}{BC^2}=\dfrac{AB^2+AC^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\left(pytago\right)\)
Giải giúp e vs ạ ,e đang cần gấp
4 tháng 10 2021
\(a,=11\sqrt{5}-6\sqrt{5}+\sqrt{5}-12\sqrt{5}=-2\sqrt{5}\\ b,=5\sqrt{3}+9\sqrt{7}-2\sqrt{3}-10\sqrt{7}=3\sqrt{3}-\sqrt{7}\\ c,=8\sqrt{3}-6\sqrt{2}+5\sqrt{2}-7\sqrt{3}=\sqrt{3}-\sqrt{2}\\ d,=\left(4\sqrt{2}-4\sqrt{3}+3\sqrt{2}\right)\sqrt{2}+4\sqrt{6}\\ =\left(7\sqrt{2}-4\sqrt{3}\right)\sqrt{2}+4\sqrt{6}=14-4\sqrt{6}+4\sqrt{6}=14\)
30 tháng 11 2023
\(3\sqrt{4x+1}+4x\sqrt{3x-2}=3x^{^2}+4x+5\Leftrightarrow12x+3+12x^2-8x=3x^2+4x+5\Leftrightarrow12x+12x^2-8x-3x^2-4x=5-3\Leftrightarrow9x^2=2\Leftrightarrow x^2=\dfrac{2}{9}\Leftrightarrow x=\dfrac{\sqrt{2}}{3}\)
Y
6 tháng 7 2023
\(VT=\sqrt{\dfrac{\sqrt{5}}{8\sqrt{5}+3\sqrt{35}}}.\left(3\sqrt{2}+\sqrt{14}\right)\)
\(=\sqrt{\dfrac{\sqrt{5}}{8\sqrt{5}+3\sqrt{5}.\sqrt{7}}}.\left(3\sqrt{2}+\sqrt{2}.\sqrt{7}\right)\)
\(=\sqrt{\dfrac{\sqrt{5}}{\sqrt{5}\left(8+3\sqrt{7}\right)}}.\left[\sqrt{2}\left(3+\sqrt{7}\right)\right]\)
\(=\sqrt{\dfrac{1}{8+3\sqrt{7}}}.\left[\sqrt{2}\left(3+\sqrt{7}\right)\right]\)
\(=\dfrac{\sqrt{2}\left(3+\sqrt{7}\right)}{\sqrt{8+3\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}.\sqrt{2}\left(3+\sqrt{7}\right)}{\sqrt{2}.\sqrt{8+3\sqrt{7}}}\) (Nhân \(\sqrt{2}\) cả tử và mẫu)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{\sqrt{16+6\sqrt{7}}}\)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{\sqrt{\left(3+\sqrt{7}\right)^2}}\)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{\left|3+\sqrt{7}\right|}\)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{3+\sqrt{7}}\)
\(=2=VP\left(dpcm\right)\)
16 tháng 4 2023
=>5x^2-6x-11=0
=>5x^2-11x+5x-11=0
=>(5x-11)(x+1)=0
=>x=11/5 hoặc x=-1
20 tháng 4 2023
Câu I:
1. \(P=\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{\sqrt{x}+1}+\dfrac{x-3}{x-1}\left(x\ge0;x\ne1\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x-1}-\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)}{x-1}+\dfrac{x-3}{x-1}\)
\(=\dfrac{x+\sqrt{x}-2x+2\sqrt{x}+x-3}{x-1}\)
\(=\dfrac{3\sqrt{x}-3}{x-1}=\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{3}{\sqrt{x}+1}\)
2. \(\dfrac{1}{P}=\dfrac{4}{3}\)
\(\Leftrightarrow\dfrac{1}{\dfrac{3}{\sqrt{x}+1}}=\dfrac{4}{3}\)
\(\Leftrightarrow\dfrac{12}{\sqrt{x}+1}=3\)
\(\Leftrightarrow3\sqrt{x}+3=12\)
\(\Leftrightarrow\sqrt{x}=3\)
\(\Leftrightarrow x=9\left(Vì.x\ge0;x\ne1\right)\)
20 tháng 4 2023
Câu II:
1. Vì đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 2, nên đường thẳng (d) cắt trục hoành tại điểm có tọa độ (2;0)
Thay x = 2; y = 0 vào phương trình đường thẳng (d), ta được:
\(0=\left(2-m\right).2+m+1\)
\(\Leftrightarrow4-2m+m+1=0\)
\(\Leftrightarrow-m=-5\)
\(\Leftrightarrow m=5\)
Vậy nếu m = 5 thì đưởng thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 2.
2. \(\left\{{}\begin{matrix}3x+2y=11\\x-2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x=12\\x-2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\3-2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm duy nhất là (x; y) = (3; 1)
10 tháng 12 2023
16:
a: ĐKXĐ: x>0
\(x+\dfrac{1}{x}+\sqrt{x}+\dfrac{1}{\sqrt{x}}=4\)
\(x+\dfrac{1}{x}>=2\cdot\sqrt{x\cdot\dfrac{1}{x}}=2\)
\(\sqrt{x}+\dfrac{1}{\sqrt{x}}>=2\cdot\sqrt{\sqrt{x}\cdot\dfrac{1}{\sqrt{x}}}=2\)
Do đó: \(x+\dfrac{1}{x}+\sqrt{x}+\dfrac{1}{\sqrt{x}}>=2+2=4\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x^2=1\\x=1\end{matrix}\right.\)
=>x=1
9 tháng 11 2023
ĐKXĐ: \(x^2+5x+2>=0\)
=>\(\left[{}\begin{matrix}x>=\dfrac{-5+\sqrt{17}}{2}\\x< =\dfrac{-5-\sqrt{17}}{2}\end{matrix}\right.\)
\(\left(x+1\right)\left(x+4\right)-3\sqrt{x^2+5x+2}=6\)
=>\(x^2+5x+4-3\sqrt{x^2+5x+2}-6=0\)
=>\(x^2+5x+2-3\sqrt{x^2+5x+2}-4=0\)(1)
Đặt \(\sqrt{x^2+5x+2}=a\)(a>=0)
Phương trình (1) trở thành:
\(a^2-3a-4=0\)
=>(a-4)(a+1)=0
=>\(\left[{}\begin{matrix}a=4\left(nhận\right)\\a=-1\left(loại\right)\end{matrix}\right.\)
=>\(x^2+5x+2=4^2=16\)
=>\(x^2+5x-14=0\)
=>\(\left(x+7\right)\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}x=-7\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)