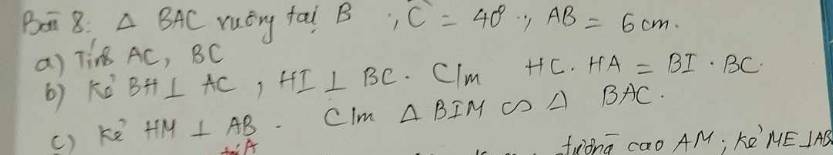TH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
1
26 tháng 10 2021
b: \(BC=\sqrt{89}\left(cm\right)\)
\(\sin\widehat{B}=\dfrac{5\sqrt{89}}{89}\)
\(\Leftrightarrow\widehat{B}\simeq32^0\)
\(\widehat{C}=58^0\)
LT
1
20 tháng 10 2023
a: ΔABC vuông tại B
=>\(\widehat{A}+\widehat{C}=90^0\)
=>\(\widehat{A}=50^0\)
Xét ΔBAC vuông tại B có
\(sinC=\dfrac{AB}{AC}\)
=>\(AC=\dfrac{6}{sin40}\simeq9,33\left(cm\right)\)
ΔBAC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC=\sqrt{9.33^2-6^2}\simeq7,14\left(cm\right)\)
b: ΔBAC vuông tại B có BH là đường cao
nên \(HC\cdot HA=BH^2\left(1\right)\)
ΔBHC vuông tại H có HI là đường cao
nên \(BI\cdot BC=BH^2\left(2\right)\)
Từ (1),(2) suy ra \(HC\cdot HA=BI\cdot BC\)
c: ΔBHA vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\left(3\right)\)
Từ (2),(3) suy ra \(BI\cdot BC=BM\cdot BA\)
=>\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)
Xét ΔBIM vuông tại B và ΔBAC vuông tại B có
\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)
Do đó: ΔBIM đồng dạng với ΔBAC
22 tháng 4 2023
cái này áp dụng hệ thức lượng thôi bạn
AH=căn 6^2-4,8^2=3,6cm
=>AC=6^2/3,6=10cm
6 tháng 3 2022
c: \(\Leftrightarrow\left\{{}\begin{matrix}8x-2\left|y+2\right|=6\\x+2\left|y+2\right|=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=9\\x+2\left|y+2\right|=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y+2\in\left\{1;-1\right\}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y\in\left\{-1;-3\right\}\end{matrix}\right.\)
a: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x-3}=2\\\dfrac{1}{2\left|y\right|-3}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3=2\\2\left|y\right|=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y\in\left\{2;-2\right\}\end{matrix}\right.\)
18 tháng 8 2023
a: \(AB=\sqrt{CA^2+CB^2}=25\left(cm\right)\)
Xét ΔABC vuông tại C có sin A=BC/BA=4/5
nên góc A\(\simeq\)53 độ
=>góc B=90-53=37 độ
ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*25=15*20=300
=>CH=12(cm)
b: ΔHCA vuông tại H có HE là đường cao
nên CE*CA=CH^2
ΔCHB vuông tại H có FH là đường cao
nên CF*CB=CH^2
=>CE*CA=CF*CB
1 tháng 2
a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMB}=90^0\)
b: Xét ΔOMC vuông tại M có MH là đường cao
nên \(HC\cdot HO=HM^2\left(1\right)\)
Xét ΔMAB vuông tại M có MH là đường cao
nên \(HA\cdot HB=HM^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)
c: Xét tứ giác AMBQ có
O là trung điểm của AB và MQ
Do đó: AMBQ là hình bình hành
Hình bình hành AMBQ có AB=MQ
nên AMBQ là hình bình hành
B2
0