
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(t,=\dfrac{3^{64}\cdot7^{24}}{7^{23}\cdot9^{66}}=\dfrac{7}{3^2}=\dfrac{7}{9}\\ u,=\dfrac{5^3\cdot3^4\cdot2^5}{5^2\cdot3^3\cdot2^4}=5\cdot3\cdot2=30\\ v,=\dfrac{3^6\cdot2^{15}}{2^6\cdot3^6\cdot2^8}=2\)

\(\left[{}\begin{matrix}x-1,7=2,3\\x-1,7=-2,3\end{matrix}\right.\left[{}\begin{matrix}x=4\\x\neg-\dfrac{3}{5}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{3}\\x+\dfrac{3}{4}=-\dfrac{1}{3}\end{matrix}\right.\left[{}\begin{matrix}x=-\dfrac{5}{12}\\x=-\dfrac{13}{12}\end{matrix}\right.\)

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

1)
a. Xét tg ABC cân tại A có AC=AB; gACB = g ABC.
Xét tg ACN và tg ABM có:
CN=BM (gt)
AC=AB
gACB=gABC
=> tg ACN = tg ABM (cgc)
=> AN=AM (2 cạnh tg ứng)
H là trung điểm BC nên AH là đường trung tuyến của tg ABC
Mak tg ABC cân => H cũng là đường cao của tg ABC => AH ⊥ BC
b. Vì H là trung đ của BC nên CH=HB=BC/2= 3cm
Áp dụng định lý Py ta go vào tg AHB có:
AB^2=AH^2+HB^2
AH^2= AB^2 - HB^2
AH^2= 5^2 - 3^2 = 16 cm
=> AH= 4 cm
c. Xét tg AMN và tg KMB có:
AM=KM (gt)
MN=BM (gt)
gHMA=gKMB (đối đỉnh)
=> tg AMN = tg KMB (cgc)
d. tg AMN = tg KMB => gMAN=gMKB
=> AN=KB=Am
Mà AB>AM (quan hệ giữ đường xiêng và hình chiếu) nên AB>BK
=> gBKA> gBAK
=> gMAN>gBAM


=)) Mik chịu á, bạn cứ làm mấy chỗ khác trước và chừa chứng minh cho mik cx đc ạ

| x - 5 | = 3 <=> x - 5 = -3 ; 3
TH1: x - 5 = 3 => x = 8
TH2: x - 5 = -3 => x = 2
Vậy x = { 8 ; 2 }


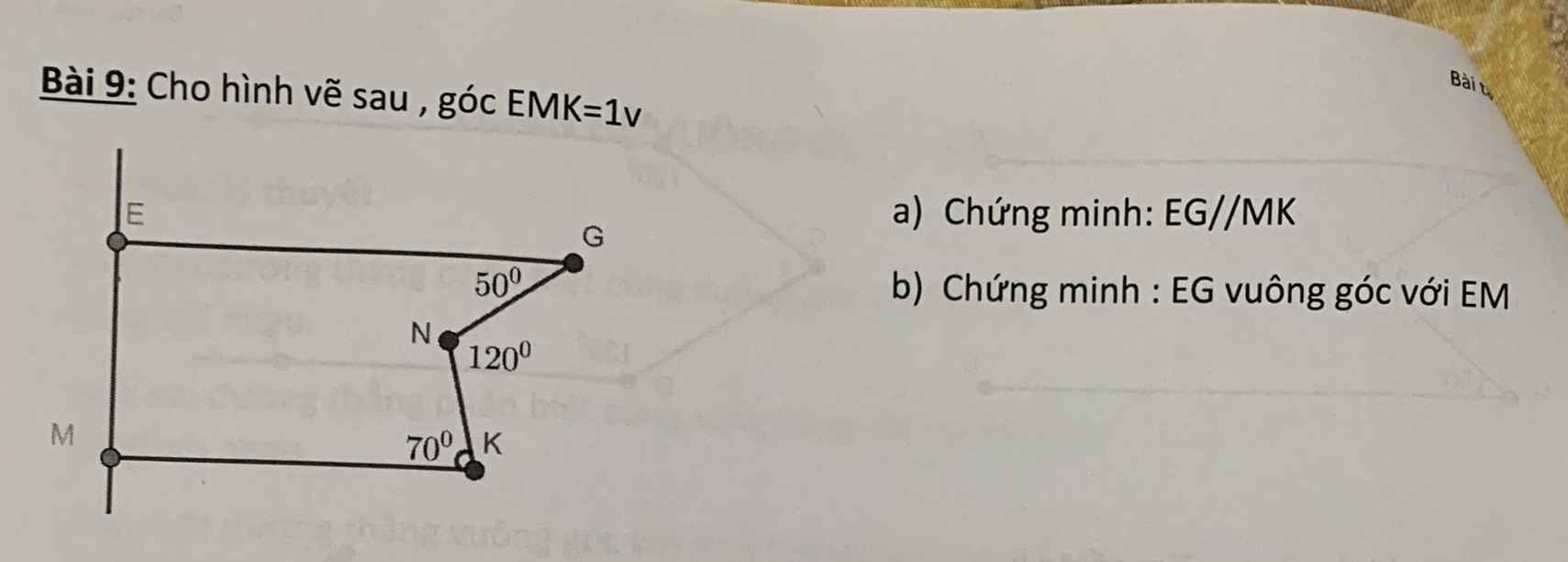
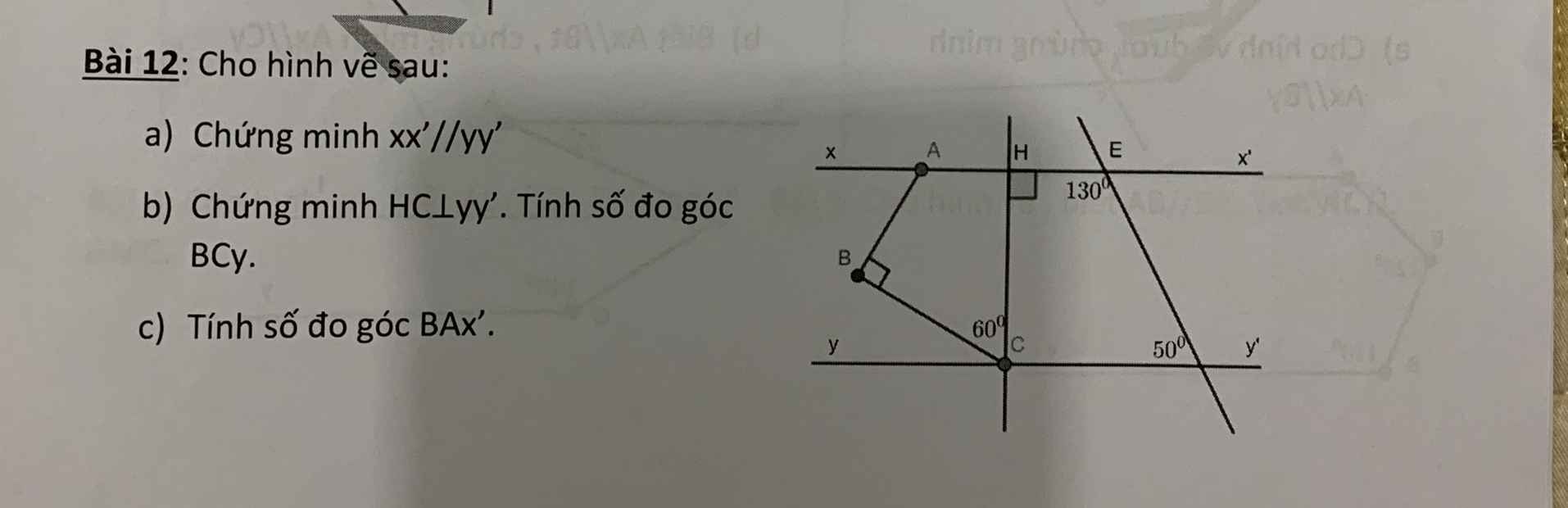




 Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
\(A=\frac{7^2}{2.9}+\frac{7^2}{9.16}+......+\frac{7^2}{86.93}+\frac{7^2}{93.100}\)
\(A=\frac{7^2}{2}-\frac{7^2}{9}+\frac{7^2}{9}-\frac{7^2}{16}+.....+\frac{7^2}{93}-\frac{7^2}{100}\)
\(A=\frac{7^2}{2}-\frac{7^2}{100}\)
\(A=....\)