Question

[Nguyễn Thanh Phong]

Giải cho tớ với các bạn ơi.Tớ đang cần gấp

Answer 1

[Ga'l wes]

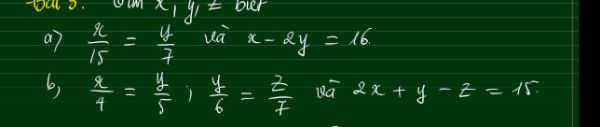
a ) \(\frac{x}{15}=\frac{y}{7}\)và \(x-2y=16\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có :

\(\frac{x}{15}=\frac{y}{7}=\frac{x}{15}=\frac{2y}{14}=\frac{x-2y}{15-14}=\frac{16}{1}=16\)

\(\Rightarrow\hept{\begin{cases}\frac{x}{15}=16\\\frac{2y}{14}=16\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=240\\y=112\end{cases}}\)

Answer 2

[Ga'l wes]

b ) Từ \(\frac{x}{4}=\frac{y}{5}\)\(\Rightarrow\)\(\frac{x}{4}.\frac{1}{6}=\frac{y}{5}.\frac{1}{6}=\frac{x}{24}=\frac{y}{30}\)( 1 )

Từ \(\frac{y}{6}=\frac{z}{7}\)\(\Rightarrow\)\(\frac{y}{6}.\frac{1}{5}=\frac{z}{7}.\frac{1}{5}=\frac{y}{30}=\frac{z}{35}\)( 2 )

Từ ( 1 ) và ( 2 ) ta có :\(\frac{x}{24}=\frac{y}{30}=\frac{z}{35}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\frac{x}{24}=\frac{y}{30}=\frac{z}{35}=\frac{2x}{48}=\frac{y}{30}=\frac{z}{35}=\frac{2x+y-z}{48+30-35}=\frac{15}{43}\)

\(\Rightarrow\hept{\begin{cases}\frac{2x}{48}=\frac{15}{43}\\\frac{y}{30}=\frac{15}{43}\\\frac{z}{35}=\frac{15}{43}\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=\frac{360}{43}\\y=\frac{450}{43}\\z=\frac{525}{43}\end{cases}}\)