
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vẽ đồ thị của hàm số 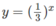 và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ x = 1/3 (H.67)
và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ x = 1/3 (H.67)
Khi x < 1/3 đồ thị của hàm số 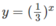 nằm phía trên đường thẳng y = 3x.
nằm phía trên đường thẳng y = 3x.
Vậy tập nghiệm của bất phương trình đã cho là (- ∞ ;1/3).

Vẽ đồ thị của hàm số y =
log
2
x
và đường thẳng y = 6 – x trên cùng một hệ trục tọa độ, ta thấy chúng cắt nhau tại điểm có hoành độ x = 4 (H.68).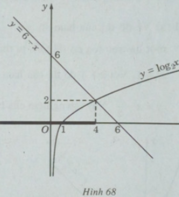 Khi x < 4, đồ thị của hàm số y =
log
2
x
nằm phía dưới y = 6 – x . Vậy tập nghiệm của bất phương trình đã cho là (-
∞
;4].
Khi x < 4, đồ thị của hàm số y =
log
2
x
nằm phía dưới y = 6 – x . Vậy tập nghiệm của bất phương trình đã cho là (-
∞
;4].

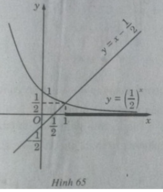
Vẽ đồ thị của hàm số 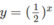 và đường thẳng
và đường thẳng 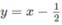 trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số
trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số 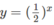 nằm phía dưới đường thẳng
nằm phía dưới đường thẳng 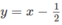 . Vậy tập nghiệm của bất phương trình đã cho là (1;+
∞
)
. Vậy tập nghiệm của bất phương trình đã cho là (1;+
∞
)

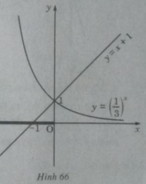
Vẽ đồ thị của hàm số  và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
Khi x < 0 đồ thị của hàm số  nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-
∞
;0]
nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-
∞
;0]

\(\Leftrightarrow2^{2x}-1+m.2^x+m\le0\\ \Leftrightarrow\left(2^x-1\right)\left(2^x+1\right)+m\left(2^x+1\right)\le0\\ \Leftrightarrow\left(2^x+1\right)\left(2^x-1+m\right)\le0\)
Vì \(2^x+1>0\forall x\) nên ta có
\(2^x-1+m\le0\Leftrightarrow2^x\le1-m\)
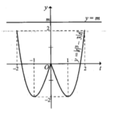
Vẽ đồ thị hàm số \(f\left(x\right)=2^x\),
ta thấy bất phương trình có nghiệm khi và chỉ khi đường thẳng y=1-m nằm trên trục Ox
\(\Rightarrow1-m>0\Leftrightarrow m< 1\) (không có dấu "=")

Đáp án A
Đặt ![]()
Yều cẩu bào toán trở thành: Tìm m để bất phương trình ![]() nghiệm đúng với mọi
nghiệm đúng với mọi ![]()
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kết quả thỏa mãn yêu cầu bài toán là ![]()

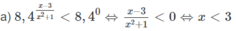
b) 2 x - 2 > 2 2 x + 1
⇔ |x−2| > 2|x+1|
⇔ x 2 − 4x + 4 > 4( x 2 + 2x + 1)
⇔ 3 x 2 + 12x < 0
⇔ −4 < x < 0
c) 2 2 x − 2. 2 x + 8 < 2 3 x . 2 1 - x
⇔ 2 2 x + 2. 2 x − 8 > 0
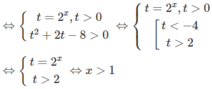
d) Đặt t = 3 x (t > 0) , ta có bất phương trình
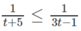
Vì vế trái dương nên vế phải cũng phải dương, tức là 3t - 1 > 0.
Từ đó ta có hệ:
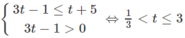
Do đó 1/3 < 3x ≤ 3. Vậy −1 < x ≤ 1.

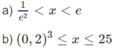
c) Bất phương trình đã cho tương đương với hệ:
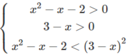
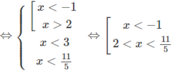
Vậy tập nghiệm là (− ∞ ; −1) ∪ (2; 11/5)
d) ln|(x − 2)(x + 4)| ≤ ln8
⇔| x 2 + 2x − 8| ≤ 8
⇔ −8 ≤ x 2 + 2x – 8 ≤ 8
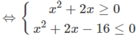
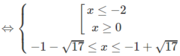
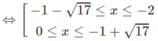
Vậy tập nghiệm là
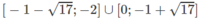
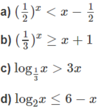

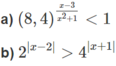
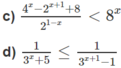
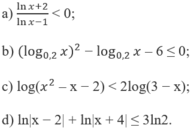
a) Vẽ đồ thị của hàm số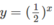 và đường thẳng
và đường thẳng 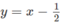 trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số
trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số 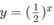 nằm phía dưới đường thẳng
nằm phía dưới đường thẳng 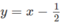 . Vậy tập nghiệm của bất phương trình đã cho là (1;+∞)
. Vậy tập nghiệm của bất phương trình đã cho là (1;+∞)
b) Vẽ đồ thị của hàm số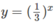 và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
Khi x < 0 đồ thị của hàm số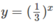 nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-∞;0]
nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-∞;0]
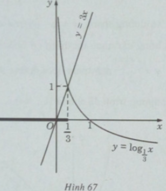
c) Vẽ đồ thị của hàm số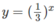 và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ x = 1/3 (H.67)
và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ x = 1/3 (H.67)
Khi x < 1/3 đồ thị của hàm số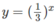 nằm phía trên đường thẳng y = 3x.
nằm phía trên đường thẳng y = 3x.
Vậy tập nghiệm của bất phương trình đã cho là (- ∞ ;1/3).
d) Vẽ đồ thị của hàm số y = log 2 x và đường thẳng y = 6 – x trên cùng một hệ trục tọa độ, ta thấy chúng cắt nhau tại điểm có hoành độ x = 4 (H.68).
Khi x < 4, đồ thị của hàm số y = log 2 x nằm phía dưới y = 6 – x . Vậy tập nghiệm của bất phương trình đã cho là (- ∞ ;4].