Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

rối quá :)
B = (-5)0 + 51 + (-5)2 + 53 + ... + (-5)2016 + 52017
B = 1 + 51 + 52 + 53 + ... + 52016 + 52017
5B = 5 + 52 + 53 + ... + 52016 + 52017
5B - B = (5 + 52 + 53 + ... + 52016 + 52017) - (1 + 51 + 52 + 53 + ... + 52016 + 52017)
4B = 52017 - 1
B = \(\dfrac{5^{2017}-1}{4}\)

1/ 3x-1 + 5.3x-1 = 162
3x-1(1 + 5) = 162
3x-1 = \(\frac{162}{6}\)
3x-1 = 27
3x-1 = 33
x - 1 = 3
x = 4
2/ B = 3100 - 399 + 398 - 397 + ... + 32 - 3 + 1
\(\Rightarrow\) 3B = 3.3100 - 3.399 + 3.398 - 3.397 + ... + 3.32 - 3.3 + 3.1
= 3101 - 3100 + 399 - 398 + ... + 33 - 32 + 3
Ta có:
4B = 3B + B = (3101 - 3100 + 399 - 398 + ... + 33 - 32 + 3) + (3100 - 399 + 398 - 397 + ... + 32 - 3 + 1)
= 3101 + 3100 - 3100 + 399 - 399 + 398 - 398 + ... + 3 - 3 + 1
= 3101 + 1
\(\Rightarrow\) B = \(\frac{3^{101}+1}{4}\)

a) \(9.3^3.\frac{1}{81}.3^2=3^2.3^3.\frac{1}{3^4}.3^2=3^7.\frac{1}{3^4}=3^3\)
b) \(4.2^5:\left(2^3.\frac{1}{16}\right)=2^2.2^5:2^3:\frac{1}{16}=2^7:2^3.16=2^4.2^4=2^8\)
c) \(3^2.2^5.\left(\frac{2}{3}\right)^2=3^2.2^5.\frac{2^2}{3^2}=2^5.2^2=2^7\)
d) \(\left(\frac{1}{3}\right)^2.\frac{1}{3}.9^2=\left(\frac{1}{3}\right)^3.\left(3^2\right)^2=\frac{1^3}{3^3}.3^4=1^3.3=3^1\)


a,(\(6x-5x^2-15+2x^3:\left(2x-5\right)\)
\(\left(2x^3-5x^2+6x-15\right):\left(2x-5\right)\)
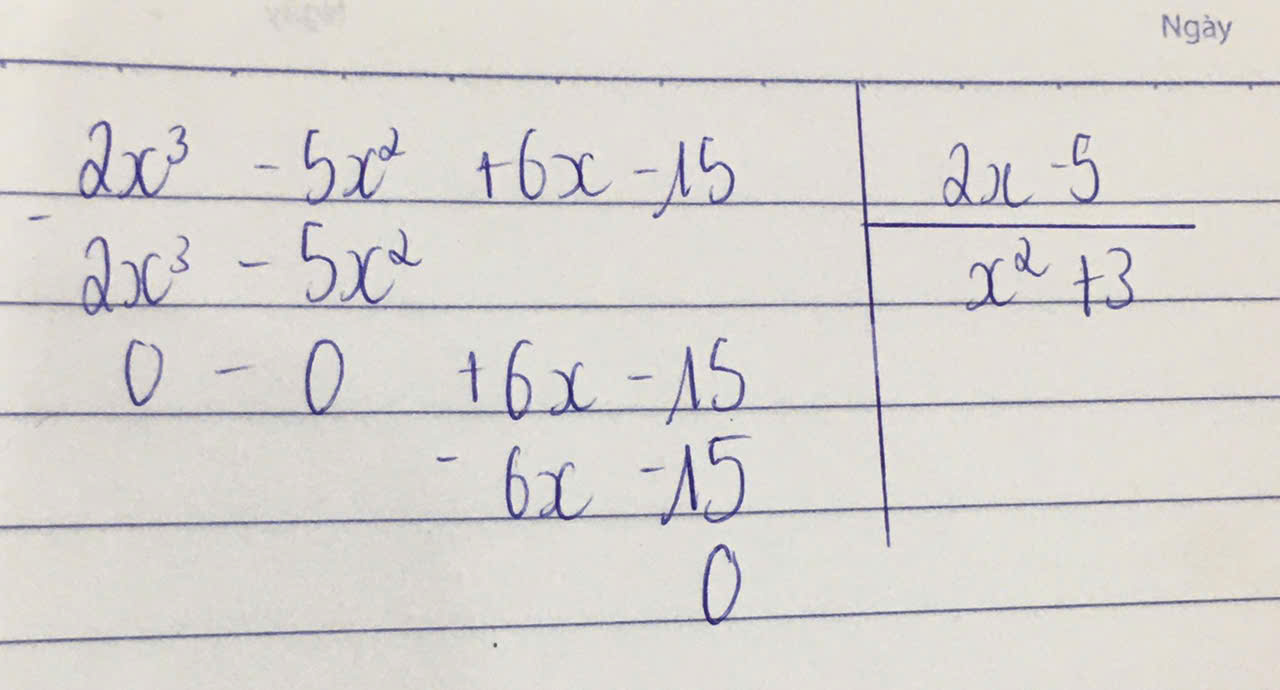

\(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}=\)
\(=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{100-99}{99.100}=\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}=1-\frac{1}{100}< 1\)
Gọi biểu thức trên là Acó:
A=1+1/2+1/2^2+1/2^3+...+1/2^99+1/2^100
2A=1/2+1/2^2+1/2^3+....+1/2^99+1/2^100+1/2^101
2A-A=(1/2+1/2^2+1/2^3+....+1/2^99+1/2^100+1/2^101)-(1+1/2+1/2^2+1/2^3+...+1/2^99+1/2^100)
A=1/2^101-1
A=-1