
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)

Lời giải:
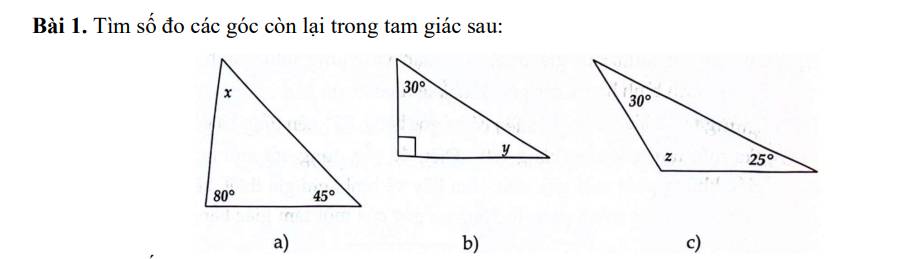
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$

Đổi 30 phút = 0,5 giờ
Quãng sông từ A đến B dài là:
\(x\) \(\times\) 0,5 + y \(\times\) 1 = 0,5\(x\) + y (km)
Kết luận Quãng đường từ A đên B dài: 0,5\(x\) + y (km)

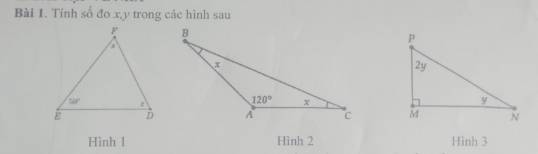
Lời giải:
Áp dụng tính chất tổng 3 góc trong 1 tam giác bằng $180^0$
Hình 1: Hình không rõ ràng. Bạn xem lại.
Hình 2: $x+x+120^0=180^0$
$2x+120^0=180^0$
$2x=60^0$
$x=60^0:2=30^0$
Hình 3:
$2y+y+90^0=180^0$
$3y=180^0-90^0=90^0$
$y=90^0:3=30^0$
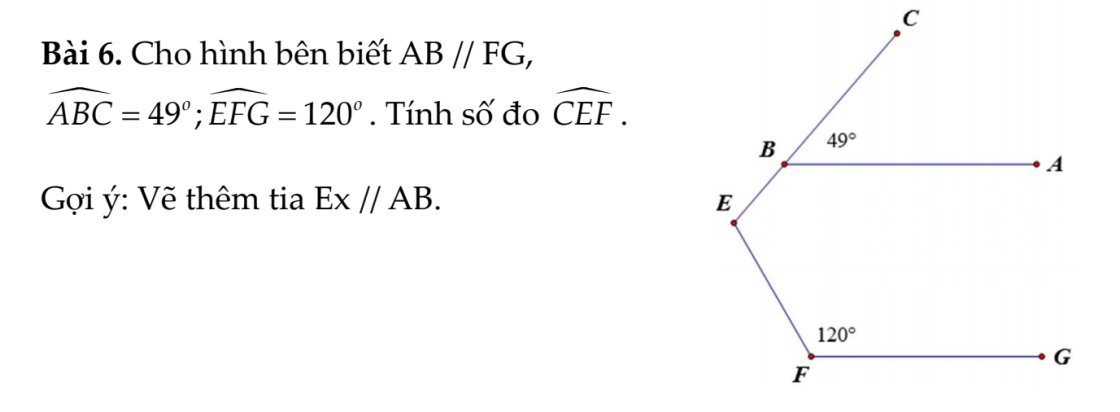
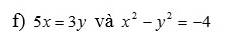


Kẻ Ex//AB(Ex và AB nằm trên cùng mặt phẳng bờ chứa tia BE)
Ta có: Ex//AB
AB//FG
Do đó: Ex//FG
Ex//AB
=>\(\widehat{BEx}=\widehat{CBA}\)(hai góc đồng vị)
=>\(\widehat{xEB}=49^0\)
Ta có: Ex//FG
=>\(\widehat{xEF}+\widehat{EFG}=180^0\)
=>\(\widehat{xEF}=180^0-120^0=60^0\)
\(\widehat{BEF}=\widehat{xEB}+\widehat{xEF}=49^0+60^0=109^0\)