Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giá trị nhỏ nhất của hàm số y = x − 3 ln x trên đoạn 1 ; e bằng
A. 1.
B. 3 − 3 ln 3.
C. e.
D. e − 3.
Đáp án D.
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số y = f x trên a ; b .
+) Giải phương trình f ' x = 0 ⇒ các nghiệm x 1 ∈ a ; b .
+) Tính các giá trị
f a ; f b ; f x i .
+) So sánh và kết luận:
m a x a ; b y = m a x f a ; f b ; f x i ; min a ; b y = min f a ; f b ; f x i
Cách giải:
ĐKXĐ: x > 0.
y = x − 3 ln x ⇒ y ' = 1 − 3 x = 0 ⇔ x = 3 ∉ 1 ; e
y 1 = 1 ; y e = e − 3 ⇒ min 1 ; e = e − 3
Đáp án A
Ta có: y ' = 1 − 1 x = 0 ⇔ x − 1 x = 0 ⇔ x = 1 . Ta có y 1 2 = 1 2 + ln 2 ; y 1 = 1 ; y e = e − 1
⇒ M a x y = e − 1 ; M i n y = 1
Đáp án B
Tập xác định D = R
Đạo hàm 
do đó hàm số đã cho luôn đồng biến trên R
Suy ra giá trị nhỏ nhất của hàm số trên đoạn [0;2] là 
Phương pháp:
- Tính y' xét tính đồng biến, nghịch biến của hàm số.
- Tính GTNN của hàm số trên [1;2]
Cách giải:
Đáp án A
Ta có: y ' = 1 − 1 x = x − 1 x ⇒ y ' = 0 ⇒ x = 1
Ta tính các giá trị của hàm số tại điểm cực trị và các điểm biên
f 1 2 = 1 2 + ln 2 ≈ 1 , 15 f 1 = 1 f e = e − 1 ≈ 1 , 72
So sánh các giá trị ta kết luận hàm số đạt GTNN và GTLN trên 1 2 ; e
Lần lượt là 1 và e − 1 .
Đáp án B
Ta có: y ' = e − x 2 x − x 2 ⇒ y ' = 0 ⇔ x = 0 x = 2
Suy ra: y − 1 = e , y 0 = 0 , y 1 = 1 e
⇒ M = e N = 0 ⇒ M + N = e
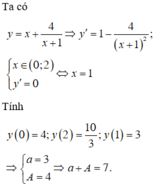
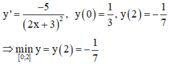
Đáp án A
Ta có: y ' = e x x 2 − x − 1 + e x 2 x − 1 = e x x 2 + x − 2 = 0 ⇔ x = 1 x = − 2
Ta có: y 0 = − 1 ; y 1 = − e ; y 2 = e 2 ⇒ M i n y 0 ; 2 = y 1 = − e