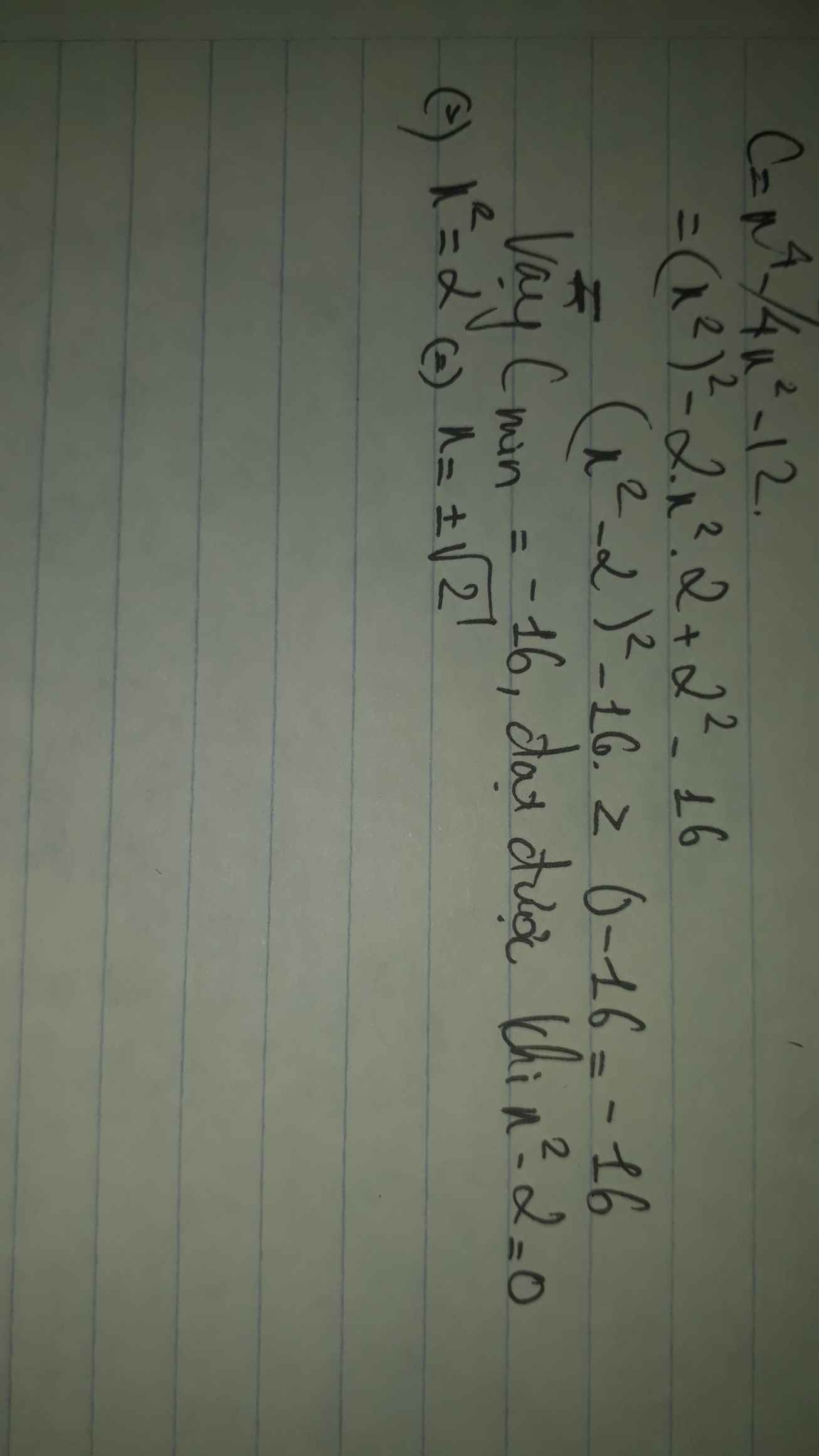Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


E=\(\left(4x^4+4x^2+1\right)-5\)
=\(\left(2x^2+1\right)^2-5\)
ta thấy \(\left(2x^2+1\right)^2\)>hoặc bằng 0 với mọi x
=>\(\left(2x^2+1\right)^2-5\)>hoặc bằng -5 với mọi x
Dấu "=" xảy ra khi 2x2+1=0<=>2x2=-1(vô lí)
VẬY ........................................
\(E=4x^4+4x^2-4\)
\(E=\left(2x^2\right)^2+4x^2+1-5\)
\(E=\left(2x^2+1\right)^2-5\)
Vì \(2x^2\ge0\Rightarrow2x^2+1\ge1\)
\(\Rightarrow\left(2x^2+1\right)^2-5\ge-4\)
Dấu = xảy ra khi \(2x^2=0\Rightarrow x=0\)
Vậy Min A = -4 khi x = 0

\(A=2x^2+4x+1=2\left(x^2+2x+1\right)-1=2\left(x+1\right)^2-1\ge-1\)
\(A_{min}=-1\) khi \(x=-1\)
Câu B chỉ có max, ko có min
\(B=-x^2+3x+4=-\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{25}{4}=-\left(x-\dfrac{3}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\)
\(B_{max}=\dfrac{25}{4}\) khi \(x=\dfrac{3}{2}\)
Câu C cũng chỉ có max, không có min
\(C=-4x^2+8x=-4\left(x^2-2x+1\right)+4=-4\left(x-1\right)^2+4\le4\)
\(C_{max}=4\) khi \(x=1\)
Câu D cũng chỉ có max, không có min
\(D=\dfrac{3}{4x^2-4x+1+4}=\dfrac{3}{\left(2x-1\right)^2+4}\le\dfrac{3}{4}\)
\(C_{max}=\dfrac{3}{4}\) khi \(x=\dfrac{1}{2}\)
(4 câu có 3 câu sai đề)
Nhầm đề bài Sorrry
đáng lẽ là ntn này giúp con dc ko ạ
\(\dfrac{3}{4x^{2_-}4x+5}\) Giúp con :(

\(4x^2+2x+12\)
\(=\left(4x^2+2x+\frac{1}{4}\right)+\frac{47}{4}\)
\(=\left[\left(2x\right)^2+2.\frac{1}{2}\left(2x\right)+\left(\frac{1}{2}\right)^2\right]+\frac{47}{4}\)
\(=\left(2x+\frac{1}{2}\right)^2+\frac{47}{4}\)
Có :
\(\left(2x+\frac{1}{2}\right)^2\ge0\)với mọi \(x\)
\(\Rightarrow\left(2x+\frac{1}{2}\right)^2+\frac{47}{4}\ge\frac{47}{4}\)
\(\Rightarrow\text{}\)GTNN của \(4x^2+2x+12\)là \(\frac{47}{4}\)
Đẳng thức xảy ra khi :
\(2x+\frac{1}{2}=0\)
\(2x=-\frac{1}{2}\)
\(x=-\frac{1}{4}\)
Vậy GTNN của \(4x^2+2x+12=\frac{47}{4}\)khi \(x=-\frac{1}{4}.\)

\(4x-x^2-12=-x^2+4x-4-8=-\left(x-4x+4\right)-8=-\left(x-2\right)^2-8\le8\)
=> GTLN của đa thức là 8
<=> x-2 = 0
<=> x = 2
\(x^2+y^2-x+6y+15\)
\(=x^2-2.x.\frac{1}{2}+\frac{1}{4}+y^2+2.y.3+9+\frac{23}{4}\)
\(=\left(x-\frac{1}{2}\right)^2+\left(y+3\right)^2+\frac{23}{4}\ge\frac{23}{4}\)
=> GTNN của đa thức là 23/4
<=> x-1/2=0 và y+3=0
<=> x=1/2 và y=-3


\(4x^2-12x+12\)
\(=\left[\left(2x\right)^2-2\cdot6x+6^2\right]-24\)
\(=\left(2x+6\right)^2-24\ge-24\)
vậy min = -24 khi và chỉ khi x=-3
\(=4\left(x^2-3x+3\right)\)
\(=4\left(\left(x^2-2.x.\frac{3}{2}+\left(\frac{3}{2}\right)^2\right)+\frac{3}{4}\right)\)
\(=4.\left(x-\frac{3}{2}\right)^2+3\)
vậy minA=3 khi x=3/2

a)
\(A=4x-x^2+3=-\left(x^2-4x-3\right)=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
Daaus = xayr ra khi: x = 2
b) \(B=4x^2-12x+15=4\left(x^2-3x+9\right)-21=4\left(x-3\right)^2-21\ge-21\)
Dấu = xảy ra khi x = 3
c) \(C=4x^2+2y^2-4xy-4y+1=\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3=\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu = xảy ra khi
2x = y và y = 2
=> x = 1 và y = 2
a) A = \(-x^2+4x+3=-\left(x-2\right)^2+7\le7\)
Dấu "=" <=> x = 2
b) \(4x^2-12x+15=\left(2x-3\right)^2+6\ge6\)
Dấu "=" xảy ra <=> \(x=\dfrac{3}{2}\)
c) \(4x^2+2y^2-4xy-4y+1\)
= \(\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3\)
= \(\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu "=" <=> \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)