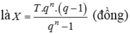Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Giá trị xe lúc mua: G(0) = 600 triệu đồng
Giá trị xe sau khi mua 5 năm : G(5) = 600 . e - 0 , 12 . 5 ≈ 329 triệu đồng

Gọi PV là giá trị hiện tại của dòng tiền thu được từ cho thuê và giá bán thanh lý. Ta có:
`PV = \frac{200}{(1+0.05)^1} + \frac{200}{(1+0.05)^2} + \frac{200}{(1+0.05)^3} + \frac{5}{(1+0.05)^3}`
`= \frac{200}{1.05} + \frac{200}{1.1025} + \frac{200}{1.1576} + \frac{5}{1.1576}`
Suy ra:
`PV ≈ 190.48 + 181.41 + 172.98 + 4.32`
<=> `PV ≈ 549.19`
Vậy, giá tối đa mà Ông Nam có thể mua chiếc xe tải là khoảng 549.19 triệu đồng.
Để xác định giá tối đa mà Ông Nam có thể mua chiếc xe tải đó, chúng ta cần tính giá trị hiện tại (PV) của dòng tiền thu được từ cho thuê và giá trị hiện tại (PV) của giá bán thanh lý sau 3 năm.
Giá trị hiện tại của dòng tiền thu được từ cho thuê hàng năm là 200 triệu đồng và sẽ kéo dài trong 3 năm. Vì lãi suất ngân hàng là 5% / năm, chúng ta có thể sử dụng công thức tính giá trị hiện tại của một chuỗi dòng tiền đều (annuity):
PV = PMT * ((1 - (1 + r)^(-n)) / r)
Trong đó: PV là giá trị hiện tại của chuỗi dòng tiền. PMT là dòng tiền hàng năm. r là lãi suất trong mỗi kỳ (tính theo tháng, quý hoặc năm). n là số kỳ (tháng, quý hoặc năm).
Áp dụng vào trường hợp này, chúng ta có: PMT = 200 triệu đồng r = 5% / năm = 0.05 n = 3 năm
Thay vào công thức, ta tính được: PV = 200 triệu * ((1 - (1 + 0.05)^(-3)) / 0.05) PV ≈ 578.19 triệu đồng
Giá trị hiện tại của giá bán thanh lý sau 3 năm là 5 triệu đồng. Chúng ta không cần điều chỉnh giá trị này vì nó đã được tính toán sau thuế.
Tổng cộng, giá trị hiện tại của chiếc xe tải là: PV_total = PV + Giá trị hiện tại giá bán thanh lý PV_total = 578.19 triệu + 5 triệu PV_total ≈ 583.19 triệu đồng
Do đó, Ông Nam chỉ có thể mua chiếc xe tải với giá tối đa khoảng 583.19 triệu đồng để đảm bảo thu hồi vốn và có lợi nhuận từ việc cho thuê xe tải trong 3 năm.

Ta có 2005 – 1985 = 20 (năm). Vậy đầu năm 2005 ứng với t = 20. Số cần tìm

Chọn đáp án A.