

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a)\(\Delta'=\left[\frac{-2.\left(m-1\right)}{2}\right]^2-m^2=m^2-2m+1-m^2=-2m+1\)
b)Để PT có hai nghiệm phân biệt thì \(\Delta'=-2m+1>0\Rightarrow m<\frac{1}{2}\)
Để PT có nghiệm kép thì: \(\Delta'=-2m+1=0\Rightarrow m=\frac{1}{2}\)
Để PT vô nghiệm thì: \(\Delta'=-2m+1<0\Rightarrow m>\frac{1}{2}\)

Chọn B.
Phương pháp:
Đưa phương trình về dạng tích, giải phương trình tìm nghiệm và tìm điều kiện để bài toán thỏa.
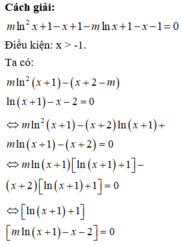
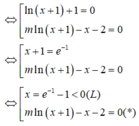

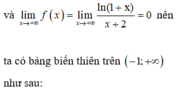


Đáp án D
BPT
( 3 m + 1 ) 9 x + ( 2 - m ) 3 x + 1 < 0 (1).
Đặt t = 3 x ( Đk : t > 0 ).
BPT trở thành:
( 3 m + 1 ) t 2 + ( 2 - m ) 3 x + 1 < 0 ⇔ ( 3 t 2 - t ) m < - t 2 - 2 t - 1 (2).
Để BPT (1) nghiệm đúng ∀ x > 0
->BPT (2) nghiệm đúng ∀ t > 1
nghiệm đúng ∀ t > 1
( vì t > 1 nên 3 t 2 - t = t ( 3 t - 1 ) > 0 )
⇔ - t 2 - 2 t - 1 3 t 2 - t > m (3) nghiệm đúng ∀ t > 1 .
* Xét f ( t ) = - t 2 - 2 t - 1 3 t 2 - t khi t > 1 :
lim x → ∞ f ( t ) = - 1 3 ;
f ' ( t ) = ( - 2 t - 2 ) ( 3 t 2 - t ) - ( - t 2 - 2 t - 1 ) ( 6 t - 1 ) ( 3 t 2 - t ) 2 = 7 t 2 + 6 t - 1 ( 3 t 2 - t ) 2 .
Ta thấy : f ' ( t ) = 0 ⇔ t = - 1 t = 1 7 ⇒ f ' ( t ) > 0 ∀ t > 1
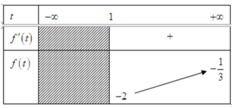
Từ BBT ta thấy: BPT (3) ) nghiệm đúng ∀ t > 1 ⇔ f ( t ) > m ∀ t > 1 ⇔ m ≤ - 2

Đáp án B



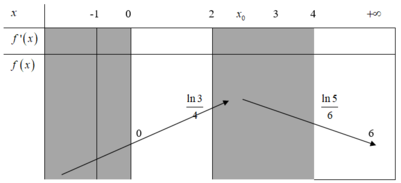
Ta có bảng biến thiên
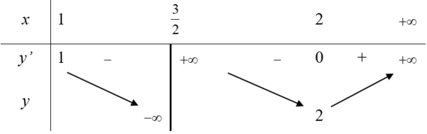
Phương trình (1) có bốn nghiệm phân biệt
⇔ * có hai nghiệm phân biệt lớn hơn 1
Mà m nguyên và m ∈ − 2019 ; 2019 nên ta có m ∈ 3 ; 4 ; ... ; 2018 .
Vậy có 2016 giá trị m thỏa mãn bài toán.

![]()
![]()
Xét hàm ![]() trên
trên ![]()

Phương trình đã cho có bốn nghiệm phân biệt khi và chỉ khi phương trình (*) có hai nghiệm phân biệt lớn hơn 1 và khác ![]()
Chọn A.

Đáp án B

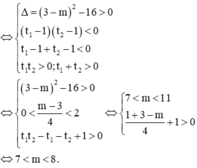
Cách 2: Thay từng giá trị của m trong các khoảng và bấm máy kiểm tra nghiệm t.