K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 11 2021
\(M=\left(\sin^210^0+\sin^280^0\right)+\left(\sin^220^0+\sin^270^0\right)-3\tan39^0\cdot\cot39^0\\ M=\left(\sin^210^0+\cos^210^0\right)+\left(\sin^220^0+\cos^220^0\right)-3\cdot1=1+1-3=-1\)
CM
10 tháng 12 2017
Vì tan α = 2 nên cos α ≠ 0
Ta có: G = 2 sin α + cos α cos α − 3 sin α = 2 sin α cos α + cos α sin α cos α cos α − 3 sin α cos α = 2 tan α + 1 1 − 3 tan α
Thay tan α = 2 ta được: G = 2.2 + 1 1 − 3.2 = − 5 5 = − 1
Vậy G = −1
Đáp án cần chọn là: D
CM
8 tháng 10 2017
Vì tan α = 2 nên cos α ≠ 0 , chia cả tử và mẫu của P cho cos α ta được:
Ta có: P = 3 sin α − 5 cos α 4 cos α + sin α = 3 sin α cos α − 5 cos α cos α 4 cos α cos α + sin α cos α = 3. tan α − 5 4 + tan α
Thay tan α = 4 ta được: P = 3.4 − 5 4 + 4 = 7 8
Vậy P = 7 8
Đáp án cần chọn là: A
NP
2
6 tháng 10 2021
Taco \(Tan\alpha=\dfrac{5}{12}\Rightarrow1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\)
\(\Leftrightarrow cos^2\alpha=\dfrac{1}{1+tan^2\alpha}=\dfrac{1}{1+\dfrac{25}{144}}=\dfrac{144}{169}\)
\(TacoN=6sin^2\alpha+7cos^2\alpha=6\left(sin^2\alpha+cos^2\alpha\right)+cos^2\alpha=6+\dfrac{144}{169}=\dfrac{1158}{169}\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 10 2021
\(tana=\dfrac{5}{12}\Rightarrow tan^2a=\dfrac{25}{144}\Rightarrow\dfrac{sin^2a}{cos^2a}=\dfrac{25}{144}\)
\(\Rightarrow\dfrac{1-cos^2a}{cos^2a}=\dfrac{25}{144}\Rightarrow cos^2a=\dfrac{144}{169}\)
\(B=6\left(sin^2a+cos^2a\right)+cos^2a=6.1+\dfrac{144}{169}=...\)
tuỳ ý giá trị biểu thức
26 tháng 10 2019
\(\left(\tan\alpha;\cot\alpha\right)=\left(a;b\right)\) cho gọn, trong đó \(b=\frac{1}{a}\)
\(B=a+b+\frac{4}{a+b}-\frac{3}{a+b}\ge2\sqrt{\frac{4\left(a+b\right)}{a+b}}-\frac{3}{a+\frac{1}{a}}\ge4-\frac{3}{2}=\frac{5}{2}\)
Dấu "=" xảy ra khi \(\tan\alpha=\cot\alpha=1\)
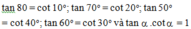
=\(30^0\)