Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích bề mặt khối gỗ thứ nhất là:
\(2\left(x\cdot2y+x\cdot z+2y\cdot z\right)=4xy+2xz+4yz\)
Diện tích bề mặt khối gỗ thứ hai là:
\(2\left(2x\cdot2y+2x\cdot3z+2y\cdot3z\right)=8xy+12xz+12yz\)
Tổng diện tích bề mặt hai khối gỗ là:
\(4xy+2xz+4yz+8xy+12xz+12yz=12xy+14xz+16yz\)

Diện tích mặt đáy của hình hộp chữ nhật là:
\((x + 1).(x + 2) = x(x + 2) + 1.(x + 2)\\ = {x^2} + 2x + x + 2 = {x^2} + 3x + 2\) \((c{m^2})\).
Vậy chiều cao của hình hộp chữ nhật đó theo x là:
\(({x^3} + 6{x^2} + 11x + 6):({x^2} + 3x + 2) = x + 3\)(cm).

Thể tích hình hộp chữ nhật là :
\(\begin{array}{l}(x + 3).(x - 1).(x - 2)\\ = \left[ {(x + 3).(x - 1)} \right].(x - 2)\\ = (x.x - 1.x + 3.x - 3.1)(x - 2)\\ = ({x^2} + 2x - 3)(x - 2)\\ = {x^2}.x - 2.{x^2} + 2x.x - 2x.2 - 3.x + 3.2\\ = {x^3} - 7x + 6\end{array}\)

Thể tích của hộp chữ nhật được tính theo công thức: V = chiều dài x chiều rộng x chiều cao.
Theo đề bài, chiều cao là 1 (cm), chiều rộng là x (cm) và chiều dài hơn chiều rộng là 3 (cm).
Do đó, chiều dài là x + 3 (cm).
Thay giá trị vào công thức, ta có:
V = (x + 3) x x x 1
= x(x + 3)
Do đó, thể tích của hộp chữ nhật được tính theo x là V = x(x + 3).
...

Tham khảo:
Ta có thể tích hình hộp chữ nhật bằng tích chiều cao và diện tích đáy
Nên chiều rộng của hình chữ nhật = thể tích : ( chiều cao . chiều dài )
Diện tích đáy là \((x + 5)(x + 1) = {x^2} + 6x + 5\)
Thay các số ở đề bài cho vào công thức trên ta được :
\( = \dfrac{{3{x^3} + 8{x^2} - 45x - 50}}{{(x + 5)(x + 1) = {x^2} + 6x + 5}} = \dfrac{{3{x^3} + 8{x^2} - 45x - 50}}{{{x^2} + 6x + 5}}\)

Vậy chiều dài hình hộp chữ nhật là 3x – 10 cm

a) \(S_{xq}=\left(a+b\right).2.h\)
mà \(\left\{{}\begin{matrix}S_{xq}=120\left(cm^2\right)\\h=60\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow120\left(a+b\right)=120\)
\(\Rightarrow a+b=1\)
\(\Rightarrow\left(a+b\right)^2=1\)
\(\Rightarrow a^2+b^2+2ab=1\)
mà \(a^2+b^2\ge2ab\) (do \(\left(a-b\right)^2=a^2+b^2-2ab\ge0,\forall ab>0\))
\(\Rightarrow4ab\le1\)
\(\Rightarrow ab\le\dfrac{1}{4}\left(1\right)\)
Để thể tích hình hộp chữ nhật có thể tích lớn nhất khi :
\(\left(ab\right)max\left(V=abh;h=60cm\right)\)
\(\left(1\right)\Rightarrow\left(ab\right)max=\dfrac{1}{4}\)
Vậy \(ab=\dfrac{1}{4}\) thỏa mãn đề bài

A...gọi hai cạnh của một hình chữ nhật lần lượt là x và y
do hình chữ nhật có diện tích là x.y= 12 (cm2 )nên công thức biểu thị sự phụ thuộc giữa một cạnh có độ dài y (cm) và cạnh kia có độ dài x (cm) của hình chữ nhật là y=\(\frac{12}{x}\)
B...gọi tương tự với cạnh đó và đường cao của nó
do diện tích của hình tam giác là \(\frac{1}{2}\)x.y=10(cm2) nên công thức biểu thị sự phụ thuộc giữa một cạnh có độ dài y (cm) và đường cao tương ứng có độ dài x (cm) của tam giác đó.là y=\(\frac{20}{x}\)

Gọi 3 cạnh của hình hộp chữ nhật lần lượt là: x; y; z ( cm; >0)
Diện tích 3 mặt lần lượt là: xy ; yz; xz ( cm^2)
( chú ý hình hộp chữ chữ nhật có 4 cạnh bằng x; 4 cạnh =y; 4 cạnh =z )
Theo bài ra ta có: \(\hept{\begin{cases}\frac{xy}{2}=\frac{yz}{3}=\frac{zx}{5}\left(1\right)\\4x+4y+4z=248\left(2\right)\end{cases}}\)
(1) => \(\frac{x}{2}=\frac{z}{3};\frac{y}{3}=\frac{x}{5}\)=> \(\frac{x}{10}=\frac{z}{15}=\frac{y}{6}\)
(2) => \(x+y+z=62\)
Tự làm tiếp nhé!
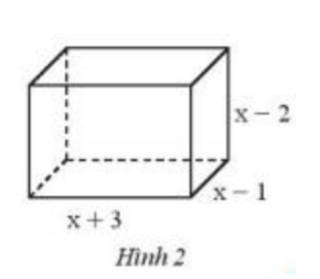
Đa thức biểu thị thể tích hình hộp chữ nhật đó là:
V = x . (x + 1) . (x – 1)
= (x.x + x.1) . (x – 1)
= (x2 + x) . (x – 1)
= x2 . (x -1) + x .(x – 1)
= x2 . x + x2 . (-1) + x.x + x . (-1)
= x3 – x2 + x2 – x
= x3 - x