Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ Ta có BC > AC > AB (7cm > 6cm > 5cm) => \(\widehat{A}>\widehat{B}>\widehat{C}\) (quan hệ giữa góc và cạnh đối diện trong tam giác)
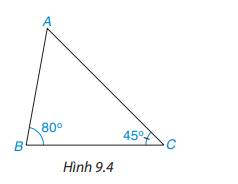
2/ Ta có \(\widehat{C}=180^o-\widehat{A}-\widehat{B}\)(tổng ba góc của một tam giác)
=> \(\widehat{C}\)= 180o - 65o - 70o = 45o
=> \(\widehat{B}>\widehat{A}>\widehat{C}\)=> AC > BC > AB (quan hệ giữa góc và cạnh đối diện trong tam giác)
3/ Ta có 18cm > 6cm + 11cm = 17cm không thoả mãn bất đẳng thức tam giác
=> Bộ ba (18cm; 6cm; 11cm) không phải là ba cạnh của một tam giác

Em dự đoán cạnh đối diện với góc B lớn hơn cạnh đối diện với góc C.

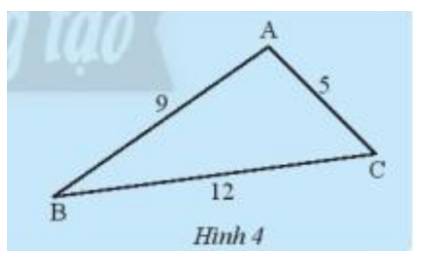
Trong tam giác ABC, xét tổng độ dài 2 cạnh so với cạnh còn lại:
\(\begin{array}{l}AB + AC = 9 + 5 > BC = 12\\AB + BC = 9 + 12 > AC = 5\\AC + BC = 12 + 5 > AB = 9\end{array}\)
Vậy tổng độ dài 2 cạnh trong 1 tam giác luôn lớn hơn độ dài cạnh còn lại.

- Ta thấy OA = OB = OC
- Trung trực ứng với cạnh BC đi qua O.


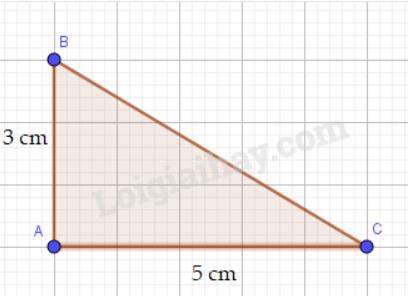
Đo độ dài các cạnh, ta được:
AB = 3,3 cm
AC = 4,6 cm
Do đó cạnh AC lớn hơn cạnh AB
Vậy dự đoán của em ở HĐ3 là đúng.