
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,=2x^2+x-2x^2-6x=-5x\\ b,=x^3+4x^2-2x-4x^2-16x+8+16-8x+x^2\\ =x^3+x^2-26x+24\\ c,=x^2-x+x^2+10x+25=2x^2+9x+25\\ d,=x^2-4-x^2+6x-9=6x-13\\ e,=x^2-1+x^2-4x+4=2x^2-4x+5\\ f,=x^2+10x+25-16+8x-x^2=18x+9\)

\(18,\\ \dfrac{1-9x^2}{x^2+4x}:\dfrac{2-6x}{3x}\left(x\ne0;x\ne-4;x\ne\dfrac{1}{3}\right)\\ =\dfrac{\left(1-3x\right)\left(1+3x\right)}{x\left(x+4\right)}\cdot\dfrac{3x}{2\left(1-3x\right)}=\dfrac{3\left(1+3x\right)}{2\left(x+4\right)}\\ \dfrac{27-x^3}{5x+10}:\dfrac{x-3}{3x+6}\left(x\ne-2;x\ne3\right)=\dfrac{\left(3-x\right)\left(x^2+3x+9\right)}{5\left(x+2\right)}:\dfrac{3\left(x+2\right)}{-\left(3-x\right)}\\ =\dfrac{-3\left(x^2+3x+9\right)}{5}\)
\(19,\\ \dfrac{4x^2}{25y^2}:\dfrac{6x}{5y}:\dfrac{2x}{9y}\left(x,y\ne0\right)=\dfrac{4x^2\cdot5y\cdot9y}{25y^2\cdot6x\cdot2x}=\dfrac{3}{5}\)

1: \(P=\dfrac{2x-5}{x\left(x-1\right)}-\dfrac{x+5}{x}+\dfrac{2x+5}{x-1}\)
\(=\dfrac{2x-5-\left(x+5\right)\left(x-1\right)+x\left(2x+5\right)}{x\left(x-1\right)}\)
\(=\dfrac{2x-5-\left(x^2+4x-5\right)+2x^2+5x}{x\left(x-1\right)}\)
\(=\dfrac{2x^2+7x-5-x^2-4x+5}{x\left(x-1\right)}\)
\(=\dfrac{x^2+3x}{x\left(x-1\right)}=\dfrac{x\left(x+3\right)}{x\left(x-1\right)}=\dfrac{x+3}{x-1}\)
2: \(x^2-1=0\)
=>\(x^2=1\)
=>\(\left[{}\begin{matrix}x=1\left(loại\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)
Thay x=-1 vào P, ta được:
\(P=\dfrac{-1+3}{-1-1}=\dfrac{2}{-2}=-1\)
3: P<1
=>P-1<0
=>\(\dfrac{x+3}{x-1}-1< 0\)
=>\(\dfrac{x+3-x+1}{x-1}< 0\)
=>\(\dfrac{4}{x-1}< 0\)
=>x-1<0
=>x<1
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x< 1\\x\ne0\end{matrix}\right.\)

\(a,P=\left[\dfrac{\left(x-1\right)^2}{x^2+x+1}-\dfrac{1-2x^2+4x}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{1}{x-1}\right]\cdot\dfrac{x\left(x^2+1\right)}{2x}\\ P=\dfrac{x^3-3x^2+3x-1-1+2x^2-4x+x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x^2+1}{2}\\ P=\dfrac{x^3-1}{x^3-1}\cdot\dfrac{x^2+1}{2}=\dfrac{x^2+1}{2}\)
\(b,\left(x+1\right)^2\ge0\Leftrightarrow x^2+2x+1\ge0\Leftrightarrow x^2+1\ge2x\\ \Leftrightarrow\dfrac{x^2+1}{2}\ge x\Leftrightarrow P\ge x\)

6: \(=x^3\left(x-2\right)-\left(x-2\right)\)
\(=\left(x-2\right)\left(x-1\right)\left(x^2+x+1\right)\)
7: =(x-4)(x+2)
2/
\(2x^3-8x=2x\left(x^2-4\right)=2x\left(x-2\right)\left(x+2\right)\)
3/
\(9x^2-\left(x-1\right)^2=\left(3x\right)^2-\left(x-1\right)^2=\left(3x-x+1\right)\left(3x+x-1\right)\)
4/
\(x^2-3x+6y-4y^2=x^2-4y^2-3x+6y=\left(x^2-4y^2\right)-\left(3x-6y\right)\)
\(=\left(x-2y\right)\left(x+2y\right)-3\left(x-2y\right)=\left(x-2y\right)\left(x+2y-3\right)\)

7: =(x-4)(x+2)
4: \(=\left(x-2y\right)\left(x+2y\right)-3\left(x-2y\right)\)
\(=\left(x-2y\right)\left(x+2y-3\right)\)

\(1,=5x\left(1-4x+4x^2\right)=5x\left(2x-1\right)^2\\ 2,=x\left(x-2y\right)-3\left(x-2y\right)=\left(x-3\right)\left(x-2y\right)\\ 3,=4x^2-\left(y+3\right)^2=\left(2x+y+3\right)\left(2x-y-3\right)\)

Bài 4:
\(P=\dfrac{4x^2-2x+7}{2x-1}=\dfrac{2x\left(2x-1\right)+7}{2x-1}=2x+\dfrac{7}{2x-1}\in Z\\ \Leftrightarrow2x-1\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\\ \Leftrightarrow x\in\left\{-3;0;1;4\right\}\\ Q=\dfrac{4x^2-2x+3}{2x-1}=\dfrac{2x\left(2x-1\right)+3}{2x-1}=2x+\dfrac{3}{2x-1}\in Z\\ \Leftrightarrow2x-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-1;0;1;2\right\}\)
Bài 5:
\(M=\dfrac{\left(5x-1\right)\left(5x+1\right)}{1-5x}+\dfrac{\left(y-3\right)\left(5x+1\right)}{y-3}=-\left(5x+1\right)+5x+1=0\)
Bài 6:
\(VT=\dfrac{a\left(a+3b\right)}{\left(a+3b\right)\left(a-3b\right)}-\dfrac{\left(2a+b\right)\left(a-3b\right)}{\left(a-3b\right)^2}=\dfrac{a}{a-3b}-\dfrac{2a+b}{a-3b}=\dfrac{-a-b}{a-3b}\)
\(VP=\dfrac{\left(a+b\right)\left(a+c\right)}{\left(a+c\right)\left(3b-a\right)}=\dfrac{a+b}{3b-a}=\dfrac{-a-b}{a-3b}\)
Vậy ta đc đpcm
 EM ĐANG CẦN GẤP, MỌI NGƯỜI GIÚP EM!!!
EM ĐANG CẦN GẤP, MỌI NGƯỜI GIÚP EM!!!
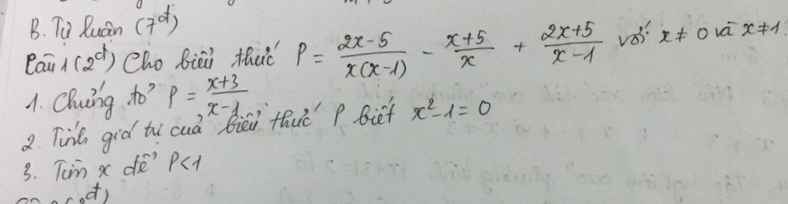 mọi người giúp em với ạ , em đang cần gấp :))
mọi người giúp em với ạ , em đang cần gấp :))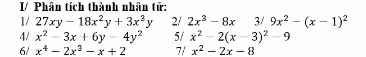



a: KM/KH=3/6=1/2
KN/KE=5/10=1/2
=>KM/KH=KN/KE
=>MN//HE
=>ΔKMN đồng dạng với ΔKHE
b: \(\dfrac{C_{KMN}}{C_{KHE}}=\dfrac{KM}{KH}=\dfrac{1}{2}\)
c: Xét tứ giác HMNI có
HM//NI
HI//MN
góc IHM=90 độ
=>HMNI là hình chữ nhật
d: Xet ΔENI vuông tại I và ΔNKM vuông tại M có
góc ENI=góc NKM
=>ΔENI đồng dạng với ΔNKM