Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Khi x=2 thì (1) sẽ là:
4-2(m+2)+m+1=0
=>m+5-2m-4=0
=>1-m=0
=>m=1
x1+x2=m+1=3
=>x2=3-2=1
b: Δ=(m+2)^2-4(m+1)
=m^2+4m+4-4m-4=m^2>=0
=>Phương trình luôn có hai nghiệm
P=(x1+x2)^2-4x1x1+3x1x2
=(x1+x2)^2-x1x2
=(m+2)^2-m-1
=m^2+4m+4-m-1
=m^2+3m+3
=(m+3/2)^2+3/4>=3/4
Dấu = xảy ra khi m=-3/2

\(\left\{{}\begin{matrix}x+2y=2\\mx-y=m\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2y=2\\2mx-2y=2m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2mx+x=2+2m\\x+2y=2\end{matrix}\right.\\ \left\{{}\begin{matrix}x\left(2m+1\right)=2\left(m+1\right)\\x+2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2\left(m+1\right)}{2m+1}\\\dfrac{2\left(m+1\right)}{2m+1}+2y=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2\left(m+1\right)}{2m+1}\\2m+2+4my+2y=4m+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2\left(m+1\right)}{2m+1}\\y\left(4m+2\right)=2m\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2\left(m+1\right)}{2m+1}\\y=\dfrac{2m}{4m+2}\end{matrix}\right.\\ thay.....x,y....vào....ta.....được\\ \dfrac{2\left(m+1\right)}{2m+1}+\dfrac{2m}{4m+2}=1\\ \Leftrightarrow\dfrac{4\left(m+1\right)}{4m+2}+\dfrac{2m}{4m+2}=\dfrac{4m+2}{4m+2}\\ \Rightarrow4m+4+2m=4m+2\\ \Leftrightarrow2m=-2\\ \Leftrightarrow m=-1\\ vậy...m=-1...thì...tm\) \(thay....m=3...vào...ta...có...hpt:\\ \left\{{}\begin{matrix}x+2y=2\\3x-y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2y=2\\6x-2y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}7x=8\\x+2y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{8}{7}\\y=\dfrac{3}{7}\end{matrix}\right.\)
\(thay...m=3....ta...có:\\ \left\{{}\begin{matrix}x+2y=2\\3x-y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2y=2\\6x-2y=6\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}7x=8\\x+2y=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{8}{7}\\y=\dfrac{3}{7}\end{matrix}\right.\\ vậy...với..m=3...thì...hệ....phương....trình....có...nghiệm...duy...nhất\left\{x=\dfrac{8}{7};y=\dfrac{3}{7}\right\}\)

Tọa độ giao điểm của (d2) và (d3) là:
\(\left\{{}\begin{matrix}2x-3y=5\\x+2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
Vì (d) song song với (d1) nên a=2
Vậy: (d): y=2x+b
Thay x=1 và y=-1 vào (d), ta được:
b+2=-1
hay b=-3

Bài 2:
\(\text{Δ}=\left[-\left(2m+1\right)\right]^2-4\cdot1\cdot2m\)
\(=\left(2m+1\right)^2-8m\)
\(=4m^2+4m+1-8m\)
\(=4m^2-4m+1=\left(2m-1\right)^2\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>\(\left(2m-1\right)^2>0\)
=>\(2m-1\ne0\)
=>\(2m\ne1\)
=>\(m\ne\dfrac{1}{2}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left[-\left(2m+1\right)\right]}{1}=2m+1\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{2m}{1}=2m\end{matrix}\right.\)
\(x_1^2+x_2^2-x_1x_2=1\)
=>\(\left(x_1+x_2\right)^2-3x_1x_2=1\)
=>\(\left(2m+1\right)^2-3\cdot2m-1=0\)
=>\(4m^2+4m+1-6m-1=0\)
=>\(4m^2-2m=0\)
=>2m(2m-1)=0
=>\(\left[{}\begin{matrix}m=0\left(nhận\right)\\m=\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMB}=90^0\)
b: Xét ΔOMC vuông tại M có MH là đường cao
nên \(HC\cdot HO=HM^2\left(1\right)\)
Xét ΔMAB vuông tại M có MH là đường cao
nên \(HA\cdot HB=HM^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)
c: Xét tứ giác AMBQ có
O là trung điểm của AB và MQ
Do đó: AMBQ là hình bình hành
Hình bình hành AMBQ có AB=MQ
nên AMBQ là hình bình hành

a: góc BDO+góc OMB=90+90=180 độ
=>BDOM nội tiếp
góc BCE=góc CAE
góc DOM+góc MBD=180 độ
góc MBD=góc NAE
=>góc DOM+góc NAE=180 độ
b: OD vuông góc BE
=>D là trung điểm của BE
ΔBEC có MD là đường trung bình
=>MD//EC
=>DF//CE
DF//CE
=>ΔNFD đồng dạng với ΔNCE
=>NF/NC=ND/NE
=>NF*NE=NC*ND

\(\orbr{\frac{1}{1-\sqrt{x}}-\frac{1}{\sqrt{x}}]}\div\orbr{\begin{cases}\\\end{cases}(2\sqrt{x}-1)(\frac{1}{1-\sqrt{x}}+\frac{\sqrt{x}}{1-\sqrt{x}+x})]}\)
sori mng em bị lag xíu
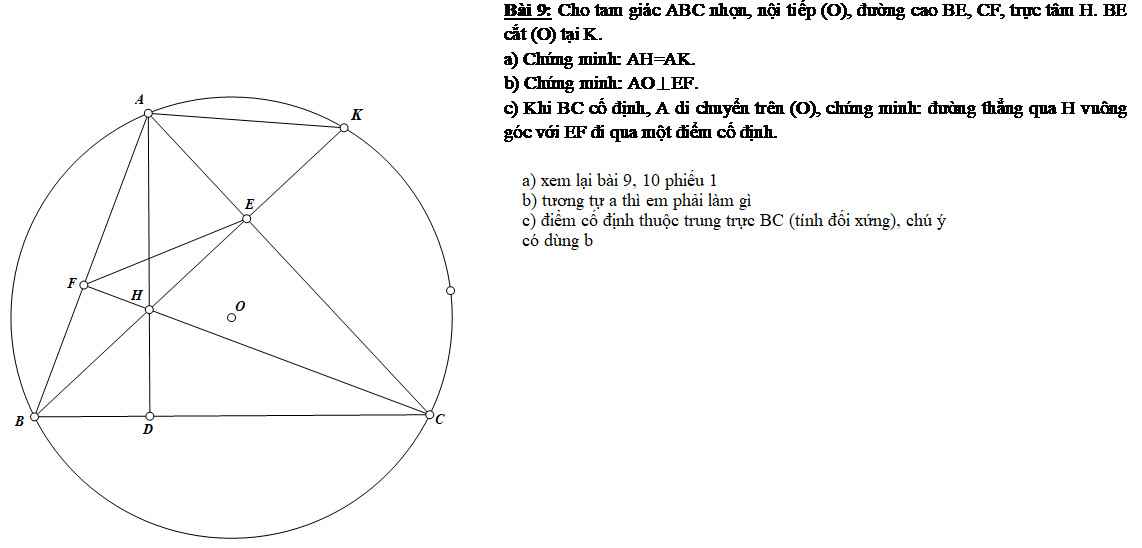
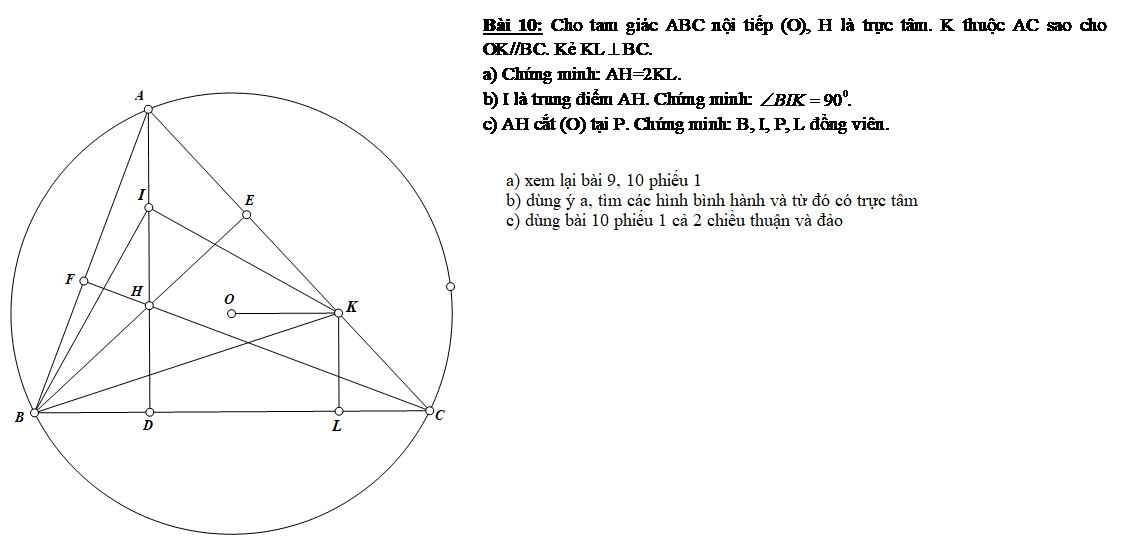



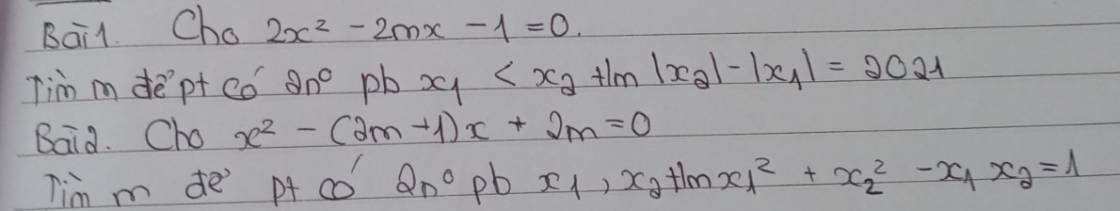
 Giúp em giải bài này với em đang cần gấp
Giúp em giải bài này với em đang cần gấp
