
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3:
a: Số học sinh của lớp là:
4+15+20+10+1=50 bạn
\(\%Xs=\dfrac{4}{50}=8\%\)
%Tốt=15/50=30%
%Khá=20/50=40%
%Đạt=10/50=20%
%Chưa đạt=1/50=2%
b: 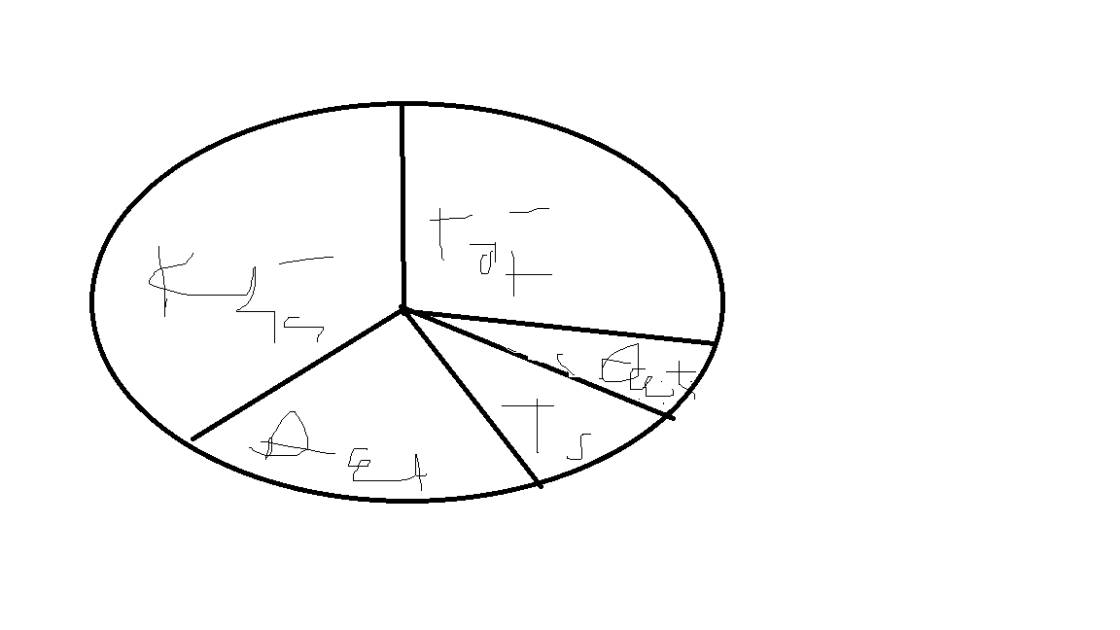



\(A\left(x\right)+B\left(x\right)=3x^4-4x^3+2x^2-3+8x^4+x^3-9x+\dfrac{2}{5}\)
\(=11x^4-3x^3+2x^2-9x-\dfrac{13}{5}\)
\(A\left(x\right)-B\left(x\right)=3x^4-4x^3+2x^2-3-8x^4-x^3+9x-\dfrac{2}{5}\)
\(=-5x^4-5x^3+2x^2+9x-\dfrac{17}{5}\)
\(B\left(x\right)-A\left(x\right)=8x^4+x^3-9x+\dfrac{2}{5}-3x^4+4x^3-2x^2+3\)
\(=5x^4+5x^3-2x^2-9x+\dfrac{17}{5}\)

a) Ta có: \(P\left(x\right)=3x^5-2x^4-2x^5-2x^2-x+3x^2+2\)
\(=x^5-2x^4+x^2+2\)
Ta có: \(Q\left(x\right)=x^5+8-5x+3x^3+3x+x^4-4x^5\)
\(=-3x^5+x^4+3x^3-2x+8\)
b) \(P\left(x\right)+Q\left(x\right)=x^5-2x^4+x^2+2-3x^5+x^4+3x^3-2x+8\)
\(=-2x^5-x^4+3x^3+x^2-2x+10\)
\(P\left(x\right)-Q\left(x\right)=x^5-2x^4+x^2+2+3x^5-x^4-3x^3+2x-8\)
\(=4x^5-3x^4-3x^3+x^2+2x-6\)

a: Xét ΔAHC vuông tại H và ΔEHC vuông tại H có
CH chung
HA=HE
=>ΔAHC=ΔEHC
b: Xét ΔAHM vuông tại H và ΔEHC vuông tại H có
HA=HE
góc HAM=góc HEC
=>ΔHAM=ΔHEC
=>HM=HC
=>H là trung điểm của MC
c: Xét tứ giác ACEM có
H là trung điểm chung của AE và MC
nên ACEM là hình bình hành
=>ME//AC
=>ME vuông góc với AB

10: Chọn B
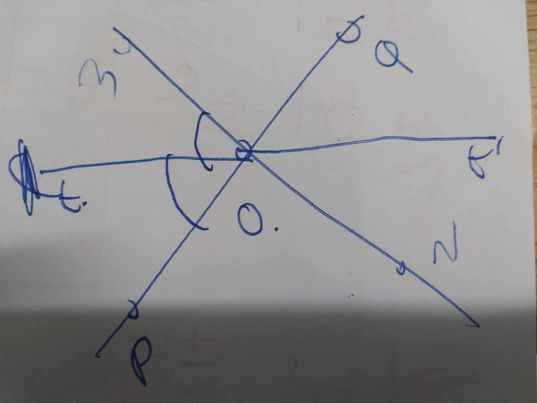
Ot là phân giác của \(\widehat{MOP}\)
=>\(\widehat{MOP}=2\cdot\widehat{tOP}\)
\(\widehat{MOP}=\widehat{NOQ}\)
=>\(\widehat{NOQ}=2\cdot\widehat{tOP}\)
mà \(\widehat{tOP}=\widehat{t'OQ}\)(hai góc đối đỉnh)
nên \(\widehat{NOQ}=2\cdot\widehat{t'OQ}\)
=>Ot' là phân giác của góc NOQ
11:
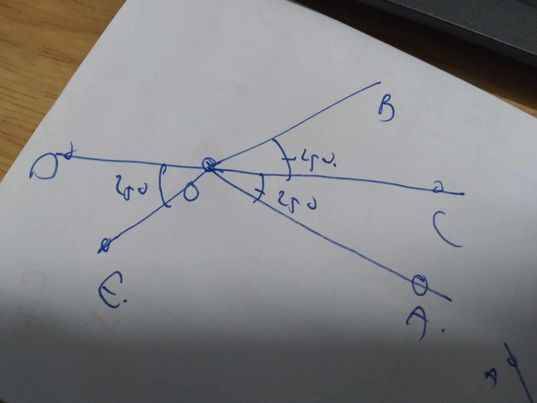
OC là phân giác của góc AOB
=>\(\widehat{AOC}=\widehat{BOC}=\dfrac{50^0}{2}=25^0\)
\(\widehat{DOE}=\widehat{BOC}\left(=25^0\right)\)
=>\(\widehat{DOE}+\widehat{DOB}=180^0\)
=>OB và OE là hai tia đối nhau
=>Hai góc đối đỉnh là \(\widehat{BOC};\widehat{DOE}\)
=>Chọn D
12:
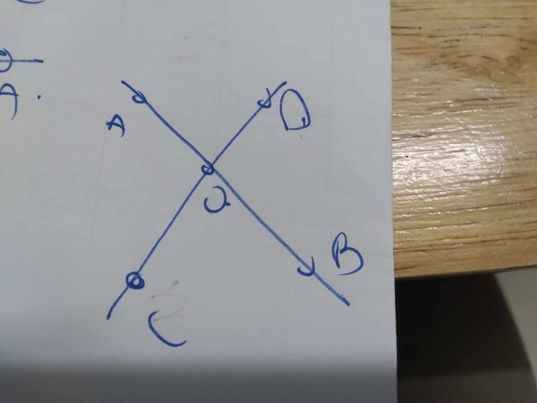
\(\widehat{AOC}+\widehat{AOD}=180^0\)
\(\widehat{AOC}-\widehat{AOD}=50^0\)
Do đó: \(\widehat{AOC}=\dfrac{180^0+50^0}{2}=115^0;\widehat{AOD}=115^0-50^0=65^0\)
=>\(\widehat{BOC}=\widehat{AOD}=65^0\)
=>Chọn B




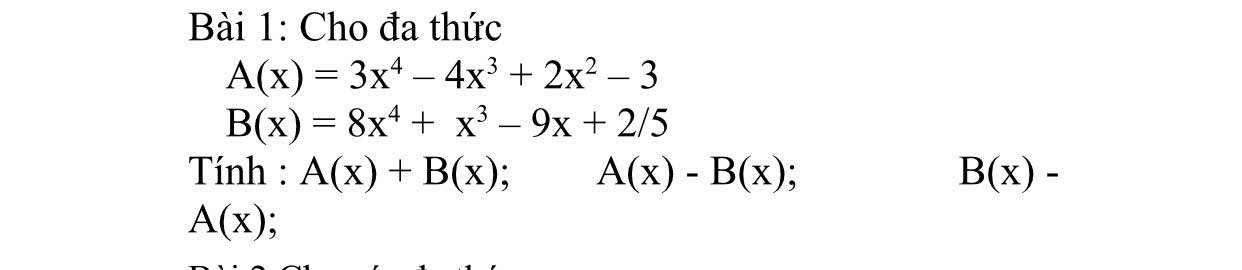


 vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))
vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))