Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(x^3+8=\left(x+2\right)\left(x^2-2x+4\right)\)
b: \(27-8y^3=\left(3-2y\right)\left(9+6y+4y^2\right)\)
c: \(y^6+1=\left(y^2+1\right)\left(y^4-y^2+1\right)\)
d: \(64x^3-\dfrac{1}{8}y^3=\left(4x-\dfrac{1}{2}y\right)\left(16x^2+2xy+\dfrac{1}{4}y^2\right)\)

Gọi giao điểm của AH và DC là I.
AF song song với DI (cùng vuông góc với AD) (1)
\(\Delta ADI=\Delta BAE\left(g.c.g\right)\Rightarrow DI=AE\) ( 2 cạnh tương ứng )
Mà \(AE=AF\left(gt\right)\Rightarrow DI=AF\) (2)
Từ (1) và (2) \(\Rightarrow AFID\)là hình bình hành.
Mà \(\widehat{FAD}=90^0\Rightarrow AFID\) là hình chữ nhật.
Từ đó: FBCI là hình chữ nhật nên IB = CF (t/c hình chữ nhật)
Gọi O là giao điểm của FC và BI \(\Rightarrow O\) là trung điểm của FC và BI
\(\Delta BHI\) vuông tại B có HO là đường trung tuyến ứng với cạnh CF nên
\(HO=\frac{1}{2}BI\Rightarrow HO=\frac{1}{2}CF\)
\(\Delta CHF\)có đường trung tuyến HO = 1/2 CF nên \(\Delta CHF\) vuông tại H.
Vậy \(\widehat{CHF}=90^0\)
Mình chỉ hướng dẫn bước thôi. Bạn tự trình bày nhé
Mong bạn hiểu lời giải. Chúc bạn học tốt.

cậu tự vẽ hình nhé
ta có ABCD là hình bình hành => AB=CD =>BE=DF
và ta có AB//CD => BE//DF
=> EBCF là hình bình hành => DE=BF(ĐPCM)
ABCD là hình bình hành nên AB =CD (cạnh đối của hình bình hành) (1)
F là trung điểm của BC (theo đầu bài) nên BF = 1/2 BC (2).
E là trung điểm của AD (theo đầu bài) nên ED = 1/2 AD (3).
Từ (1), (2) và (3) suy ra BF = ED (4).
BF // ED (vì F nằm trên AB, E nằm trên AD; BC và AD là cạnh đối của hình bình hành ABCD nên BC//AD) (5).
Từ (4) và (5) suy ra BFDE là hình bình hành (2 cạnh đối song song và bằng nhau) =>BE = DF (điều phải chứng minh)

a:
ABCD là hình thoi
=>\(\widehat{C}+\widehat{B}=180^0\) và \(\widehat{B}=\widehat{D}=60^0\)
=>\(\widehat{C}=180^0-60^0=120^0\)
Xét ΔAFB vuông tại F và ΔAED vuông tại E có
AB=AD
\(\widehat{B}=\widehat{D}\)
Do đó: ΔAFB=ΔAED
=>AF=AE và BF=ED
Xét tứ giác AECF có
\(\widehat{AEC}+\widehat{AFC}+\widehat{C}+\widehat{FAE}=360^0\)
=>\(\widehat{FAE}+120^0+90^0+90^0=360^0\)
=>\(\widehat{FAE}=60^0\)
Xét ΔAEF có AE=AF và \(\widehat{FAE}=60^0\)
nên ΔAEF đều
b: CE+ED=CD
CF+FB=CB
mà CD=CB và ED=FB
nên CE=CF
Xét ΔCBF có \(\dfrac{CE}{CD}=\dfrac{CF}{CB}\)
nên EF//BD

d. 2x2(x - y) + 2y(y - x)
= 2x2(x - y) - 2y(x - y)
= (2x2 - 2y)(x - y)
= 2(x2 - y)(x - y)
e. 5a2b(a - 2b) - 2a(2b - a)
= 5a2b(a - 2b) + 2a(a - 2b)
= (5a2b + 2a)(a - 2b)
= a(5ab + 2)(a - 2b)
f. 4x2y(x - y) + 9xy2(x - y)
= (4x2y + 9xy2)(x - y)
= xy(4x + 9y)(x - y)
g. 50x2(x - y)2 - 8y2(y - x)2
= 50x2(x2 - 2xy + y2) - 8y2(y2 - 2xy + x2)
= 50x2(x2 - 2xy + y2) - 8y2(x2 - 2xy + y2)
= 50x2(x - y)2 - 8y2(x - y)2
= (50x2 - 8y2)(x - y)2
= 2(25x2 - 4y2)(x - y)2.

c: \(\Leftrightarrow\dfrac{x}{2012}-1+\dfrac{x+1}{2013}-1+\dfrac{x+2}{2014}-1+\dfrac{x+3}{2015}-1+\dfrac{x+4}{2016}-1=0\)
=>x-2012=0
hay x=2012
d: \(\Leftrightarrow\dfrac{x-90}{10}-1+\dfrac{x-76}{12}-2+\dfrac{x-58}{14}-3+\dfrac{x-36}{16}-4+\dfrac{x-15}{17}-5=0\)
=>x-100=0
hay x=100

Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
=>AEDF là hình chữ nhật
Hình chữ nhật AEDF có AD là phân giác của \(\widehat{FAE}\)
nên AEDF là hình vuông

1/(x+2)2 -(3x-1)2=(x+2+3x-1)(x+2-3x+1)=4x(-2x+3)=-8x2+12x
2/(x4+x2)(-2x3-2x)=x2(x2+1)-2x(x2+1)=(x2+1)(x2-2x)
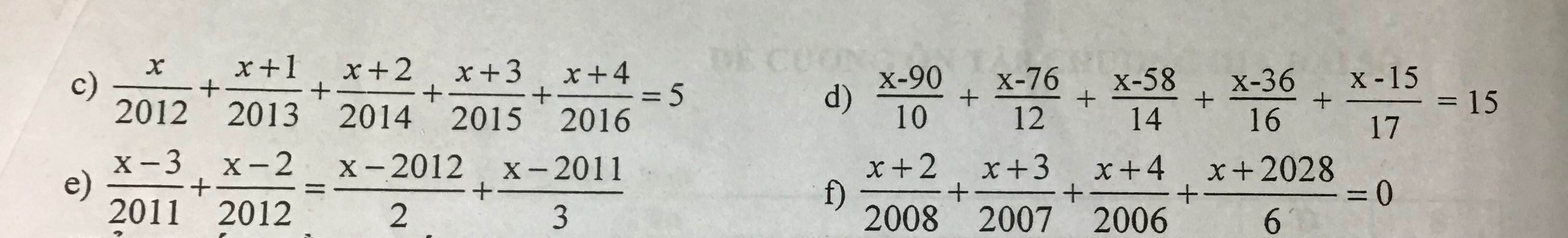 Giúp mình d,e,f với ạ !!!! Mình cảm ơn
Giúp mình d,e,f với ạ !!!! Mình cảm ơn
đề bài:Biến đổi các biểu thức sau thành tích các đa thức:
e) \(125x^6-27y^9=\left(5x^2\right)^3-\left(3y^3\right)^3=\left(5x^2-3y^3\right)\left(25x^4+15x^2y^3+9y^6\right)\)
f) \(x^9-27y^3=\left(x^3\right)^3-\left(3y\right)^3=\left(x^3-3y\right)\left(x^6+3x^3y+9y^2\right)\)