Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Vì (d) có hệ số góc là 3 nên a=3
Vậy: (d): y=3x+b
Thay x=-2 và y=4 vào (d), ta được:
\(b-6=4\)
hay b=10
b: Vì (d)//y=3x-2 nên a=3
Vậy: (d): y=3x+b
Thay x=-3 và y=-2 vào(d), ta được:
\(b-9=-2\)
hay b=7

a. Để d đi qua A; B
\(\Leftrightarrow\left\{{}\begin{matrix}5=2a+b\\-1=-a+b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)
b. Theo câu a pt AB có dạng: \(y=2x+1\)
Thế tọa độ C vào pt AB ta được:
\(9=2.4+1\) (thỏa mãn)
Vậy C thuộc AB hay 3 điểm A;B;C thẳng hàng
c. Gọi M là tọa độ giao điểm của AB và Ox
\(\Rightarrow0=2x_M+1\Rightarrow x_M=-\dfrac{1}{2}\Rightarrow OM=\left|x_M\right|=\dfrac{1}{2}\)
Gọi N là giao điểm của AB và Oy
\(\Rightarrow y_N=2.0+1\Rightarrow y_N=1\Rightarrow ON=1\)
Gọi H là hình chiếu vuông góc của O lên AB \(\Rightarrow OH=d\left(O;AB\right)\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{OH^2}=\dfrac{1}{ON^2}+\dfrac{1}{OM^2}=\dfrac{1}{1^2}+\dfrac{1}{\left(\dfrac{1}{2}\right)^2}=5\)
\(\Rightarrow OH=\dfrac{\sqrt{5}}{5}\)

Đường thẳng ax – by = 4 đi qua hai điểm A(4; 3), B(-6; -7) nên tọa độ của A và B nghiệm đúng phương trình đường thẳng.
*Với điểm A: 4a – 3b = 4
*Với điểm B: -6a + 7b = 4
Hai số a và b là nghiệm của hệ phương trình: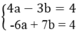
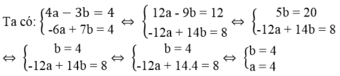
Vậy a = 4, b = 4.

a.
Gọi d là đường thẳng đi qua A, B. Do A; B đều thuộc d nên tọa độ A; B phải thỏa mãn pt d
\(\Leftrightarrow\left\{{}\begin{matrix}-5=a.0+b\\-1=-1.a+b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-4\\b=-5\end{matrix}\right.\)
b.
Câu b đề sai, 4 điểm này không hề thẳng hàng (thay tọa độ C, D vào pt d đều không thỏa mãn)

Đường thẳng y = (m – 2)x + n (d) đi qua hai điểm A(-1;2) và B(3; -4). Khi đó tọa độ các điểm A, B thỏa mãn (d), nghĩa là:
2 = (m – 2)(-1) + n (1)
và -4 = (m – 2).3 + n (2)
Rút gọn hai phương trình (1) và (2), ta được
-m + n = 0; (1’)
3m + n = 2. (2’)
Từ (1’) suy ra n = m. Thay vào (2’), ta có 3m + 3 = 2 suy ra m = 1/2.
Trả lời: Khi m = n = 1/2 thì (d) đi qua hai điểm A và B đã cho.

1, - Xét phương trình hoành độ giao điểm :\(2x^2=ax+b\)
\(\Rightarrow2x^2-ax-b=0\left(I\right)\)
Mà (P) tiếp xúc với d .
Nên PT ( I ) có duy nhất một nghiệm .
\(\Leftrightarrow\Delta=\left(-a\right)^2-4.2.\left(-b\right)=a^2+8b=0\)
Lại có : d đi qua A .
\(\Rightarrow b+0a=-2=b\)
\(\Rightarrow a=4\)
2. Tương tự a
3. - Xét phương trình hoành độ giao điểm :\(2x^2=2m+1\)
\(\Rightarrow2x^2-2m-1=0\)
Có : \(\Delta^,=\left(-m\right)^2-\left(-1\right).2=m^2+3\)
=> Giao điểm của P và d là : \(\left\{{}\begin{matrix}x_1=\dfrac{m+\sqrt{m^2+3}}{2}\\x_2=\dfrac{m-\sqrt{m^2+3}}{2}\end{matrix}\right.\)

ĐTHS y=ax+6 đi qua điểm M(1,2) nên ta có x=1,y=2
Thay x=1,y=2 vào đồ thị y=ax+6 ta có : 2=a.1+6⇒a=-4
Vậy ĐTHS có dạng y=-4x+6
chúc bn hok tốt ![]()

theo bài ra ta có hệ pt: \(\left\{{}\begin{matrix}-4=3a+b\\2=-a+b\end{matrix}\right.< =>\left\{{}\begin{matrix}a=-\dfrac{3}{2}\\b=\dfrac{1}{2}\end{matrix}\right.\)
\(=>a+b=-\dfrac{3}{2}+\dfrac{1}{2}=-1\)