Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Xét đường thẳng Δ: 3x - 2y - 7 = 0 và d1: 3x + 2y = 0 ta có:
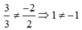

Ta có d 2 : 3 x − 2 y + 1 = 0 ⇔ 6 x − 4 y + 2 = 0
Ta có điểm A(-1; 1) thuộc đường thẳng d2,.
Vì hai đường thẳng d1 và d2 song song với nhau nên ta có:
d ( d 1 ; d 2 ) = d ( A ; d 1 ) = 6. ( − 1 ) − 4. ( − 1 ) + 5 6 2 + ( − 4 ) 2 = 3 52
ĐÁP ÁN D

a) Tọa độ giao điểm của hai đường thẳng \({d_1},{d_2}\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}3x + 2y - 5 = 0\\x - 4y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{9}{7}\\y = \frac{4}{7}\end{array} \right.\)
Hệ phương trình có nghiệm duy nhất nên 2 đường thẳng cắt nhau.
b) Tọa độ giao điểm của hai đường thẳng \({d_3},{d_4}\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x - 2y + 3 = 0\\ - 2x + 4y + 10 = 0\end{array} \right.\) .
Hệ phương trình vô nghiệm.nên 2 đường thẳng song song với nhau
c) Tọa độ giao điểm của hai đường thẳng \({d_5},{d_6}\) tương ứng với t thỏa mãn phương trình:
\(4\left( { - \frac{1}{2} + t} \right) + 2\left( {\frac{5}{2} - 2t} \right) - 3 = 0 \Leftrightarrow 0t = 0\) .
Phương trình này có nghiệm với mọi t. Do đó \({d_5} \equiv {d_6}\).

a) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = 3,b = 4,c = 21\)
Ta có \({a^2} + {b^2} - c = 9 + 16 - 21 = 4 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I(3;4)\) và có bán kính \(R = \sqrt 4 = 2\)
b) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = 1,b = - 2,c = 2\)
Ta có \({a^2} + {b^2} - c = 1 + 4 - 2 = 3 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I(1; - 2)\) và có bán kính \(R = \sqrt 3 \)
c) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = \frac{3}{2},b = - 1,c = 7\)
Ta có \({a^2} + {b^2} - c = \frac{9}{4} + 1 - 7 = - \frac{{15}}{4} < 0\). Vậy đây không là phương trình đường tròn.
d) Phương trình không có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) nên phương trình đã cho không là phương trình đường tròn.

Đáp án B
Do điểm M nằm trên trục hoành nên M( x; 0)
Khoảng cách từ M đến mỗi đường thẳng lần lượt là:
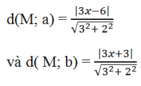
Theo bài ra ta có: d( M; a) = d( M; b) nên
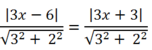
Do đó: ![]()
Sut ra 3x- 6= -3x-3 nên x= 1/2
Vậy điểm M ( 1/2; 0)

Giao điểm A của d1 và d2 là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-2y+5=0\\2x-3y+7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow A\left(1;3\right)\)
Do \(d//d_3\Rightarrow d\) nhận \(\overrightarrow{n_d}=\left(3;4\right)\) là 1 vtpt
Phương trình d:
\(3\left(x-1\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-15=0\)

Xét phương án A ta có:
Do đó; đường thẳng ∆ cắt đường thẳng 3x+ 2y+ 4= 0.
Chọn A.