Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

@soyeon_Tiểubàng giải
Trần Việt Linh
Silver bullet
mn giúp mk vs!
còn nhiều btập lắm ! làm ơn~!
https://hoc24.vn/hoi-dap/question/100664.html
Bạn tham khảo nhé

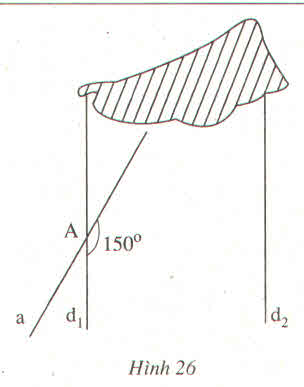
Ta có : ˆA1A1^ và ˆA2A2^ là hai góc kề bù nên:
ˆA1+ˆA2=1800⇒ˆA2=1800−ˆA1=1800−1500=300A1^+A2^=1800⇒A2^=1800−A1^=1800−1500=300
Vì d1 // d2 và ˆA2A2^ so le trong với ˆB1B1^
⇒ˆB1=ˆA2=300⇒B1^=A2^=300
Vậy ˆB1=300
Gọi B giao điểm của a và d2.
d1 // d2 nên góc nhọn tại B bằng góc nhọn tại A và bằng
1800 - 1500= 300.

Hình 1: ta có: \(\hat{NAI}=\hat{AID}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//DH
Ta có: \(\hat{AID}=\hat{AKM}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên DH//MK
Ta có: AN//DH
DH//MK
Do đó: AN//DH//MK
Hình 2:
Ta có: \(\hat{N}+\hat{H}=70^0+110^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên MN//HK

AB//MN ⇒ góc BAO + góc AON = 180 độ (trong cùng phía)
⇒ góc AON = 180 độ - góc BAO = 180 độ - 120 độ = 60 độ
MN//CD ⇒ góc NOC + góc OCD = 180 độ (trong cùng phía)
=. góc NOC= 180 độ - góc OCD = 180 độ - 140 độ = 40 độ
ta có góc AON = 60 độ, mà góc NOC = 40 độ
vậy ON không phải là phân giác của góc AOC

Ta có tam giác ABC vuông ở A nên
\(\widehat{ABC}+\widehat{C}_1=90^0\)
Trong đó tam giác OCD vuông ở D có \(\widehat{MOP}=\widehat{C}_2=90^0\)
Nên \(\widehat{MOP}=\widehat{ABC}\)
\(\widehat{MOP}=32^0\)
Ta có tam giác ABC vuông ở A nên ∠ABC + ∠BCA = 900
Trong đó tam giác OCD vuông ở D có ∠COD + ∠OCD = 900
mà góc ∠BCA = ∠OCD ( 2 góc đối đỉnh)
Từ (1),(2),(3) ∠COD = ∠ABC mà ∠ABC= 320 . Nên ∠COD = 320
hay chính là ∠MOP =320

a) trong hình a ta có tam giác ABC là tam giác vuông (B là góc vuông)
suy ra A+C=90* (hai góc nhọn phụ nhau) hay 45*+C= 90*
suy ra C=90*- 45*=45*
tìm góc E thì bạn làm theo các bước như tìm góc C
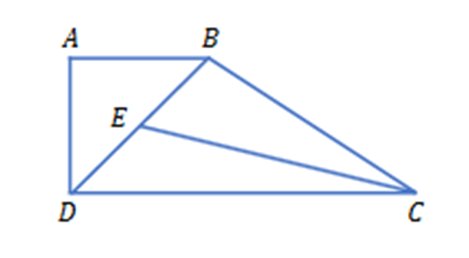






Góc nhọn: \(\widehat{ABD};\widehat{ADB};\widehat{BEC};\widehat{EDC};\widehat{BDC};\widehat{ECD};\widehat{BCE};\widehat{BCD}\)
Góc vuông: \(\widehat{BAD}\)
Góc tù: \(\widehat{DBC};\widehat{EBC};\widehat{DEC}\)
a, Góc nhọn: \(\widehat{ABD}\); \(\widehat{BCE}\); \(\widehat{BCD}\); \(\widehat{DCE}\); \(\widehat{BDC}\); \(\widehat{ADB}\); \(\widehat{BEC}\)
b, Góc vuông: \(\widehat{BAD}\); \(\widehat{ADC}\)
c, Góc tù: \(\widehat{ABC}\); \(\widehat{CBD}\); \(\widehat{CED}\)