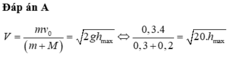Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

h 0 A I
Một vật rơi từ độ cao h xuống đĩa thì vận tốc lúc chạm đĩa tại O của vật cũng chính là vận tốc lớn nhất của con lắc dao động thỏa mãn:
\(v_{max}^2 - v_0^2 = 2gh\)
=> \(v_{max} = \sqrt{2gh} = \sqrt{2.10.1} = \sqrt{20} (m/s)\)
Mà: \(v_{max} = A \omega=> A = \frac{v_{max}}{\omega} = \frac{\sqrt{20}}{10} \approx0,447m.\)
Lực kéo lớn nhất tác dụng lên điểm I chính là lực đàn hồi lớn nhất khi lò xo dãn.nhiều nhất.(ở vị trí biên A)
\(F_ {maxI} = kA = 10.0,447 = 4,47N.\)
Chọn đáp án.B.

a) Từ định luật bảo toàn cơ năng ta có:
\(\frac{1}{2}mv^2_0=\frac{1}{2}kA^2\)
\(\Rightarrow A=v_0\sqrt{\frac{m}{k}}=2\sqrt{\frac{1}{1600}}=0,05m=5cm\)
b) Phương trình dao động có dạng: \(x=A\cos\left(\omega t+\varphi\right)\)
Tần số góc: \(\omega=\sqrt{\frac{k}{m}}=\frac{1600}{1}=40rad\text{/s }\)
Tại \(t=0\)\(\begin{cases}x=0=A\cos\varphi\\v=-2=-\omega A\sin\varphi\end{cases}\)\(\Rightarrow\varphi=\frac{\pi}{2}\)
Phương trình dao động: \(x=5\cos\left(40t+\frac{\pi}{2}\right)\left(cm\right)\)

Áp dụng định luật bảo toàn động lượng cho quá trình đạn va chạm với bao cát:
\(m\cdot v=\left(M+m\right)\cdot V\)
\(\Rightarrow m\cdot v=\left(M+m\right)\cdot\sqrt{2gh}\)
\(\Rightarrow0,1\cdot500=\left(20+0,1\right)\cdot\sqrt{2\cdot10\cdot h}\)
\(\Rightarrow h=0,31m=31cm\)

Dùng công thức độc lập
\(x^2+\frac{v^2}{\omega^2}=A^2\)
Ta có:
\(\begin{cases}3^2+\frac{\left(8\pi\right)^2}{\omega^2}=A^2\\4^2+\frac{\left(6\pi\right)^2}{\omega^2}=A^2\end{cases}\)\(\Leftrightarrow\begin{cases}A=5\\\omega=2\sqrt{10}\end{cases}\)
\(\Rightarrow T=\frac{2\pi}{\omega}=1\left(s\right)\\ 2s=2T\Leftrightarrow S=8A=40cm\)