Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
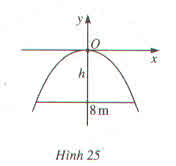
Parabol nhận trục tung là trục đối xứng
(điểm thấp nhất thuộc đồ thị có tọa độ A(4,ya)
\(y\left(4\right)=-\dfrac{1}{2}.4^2=-8\)
Vậy chiều cao cổng là 8m

Ta có : \(0< \alpha< \dfrac{\pi}{2}\)
=> \(\sin\alpha>0,\cos\alpha>\text{0},\tan\alpha>\text{0},\cot\alpha>\text{0}\)
a, Ta có : \(\sin\left(\alpha-\pi\right)=-\sin\left(\pi-\alpha\right)=-\left[-\sin\left(\alpha\right)\right]=\sin\alpha\)
=> \(sin\left(\alpha-\pi\right)>\text{0}\)
b, \(\cos\left(\dfrac{3\pi}{2}-\alpha\right)=\cos\left(\pi+\dfrac{\pi}{2}-\alpha\right)=-\cos\left(\dfrac{\pi}{2}-\alpha\right)=-sin\alpha\)
=> \(\cos\left(\dfrac{3\pi}{2}-\alpha\right)< \text{0}\)
c, \(tan\left(\alpha+\pi\right)=tan\alpha\)
=> \(tan\left(\alpha+\pi\right)>\text{0}\)
d, \(cot\left(\alpha+\dfrac{\pi}{2}\right)=-tan\alpha\)
=> \(cot\left(\alpha+\dfrac{\pi}{2}\right)< \text{0}\)

C1:
\(A=\dfrac{10^{50}+2}{10^{50}-1}=\dfrac{10^{50}-1}{10^{50}-1}+\dfrac{3}{10^{50}-1}=1+\dfrac{3}{10^{50}-1}\\ B=\dfrac{10^{50}}{10^{50}-3}=\dfrac{10^{50}-3}{10^{50}-3}+\dfrac{3}{10^{50}-3}=1+\dfrac{3}{10^{50}-3}\\ \text{Vì }10^{50}-3< 10^{50}-1\Rightarrow\dfrac{3}{10^{50}-3}>\dfrac{3}{10^{50}-1}\Rightarrow1+\dfrac{3}{10^{50}-3}>1+\dfrac{3}{10^{50}-1}\Leftrightarrow B>A\)
Vậy \(B>A\)
C2: Áp dụng \(\dfrac{a}{b}>1\Rightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\left(n>0\right)\)
Dễ thấy
\(B=\dfrac{10^{50}}{10^{50}-3}>1\\ \Rightarrow B=\dfrac{10^{50}}{10^{50}-3}>\dfrac{10^{50}+2}{10^{50}-3+2}=\dfrac{10^{50}+2}{10^{50}-1}=A\)
Vậy \(B>A\)

c)
I)
\(\frac{1}{6},\frac{1}{3},\frac{1}{2},\frac{2}{3},...\)
Quy đồng:
\(\frac{1}{6},\frac{2}{6},\frac{3}{6},\frac{4}{6},...\)
=> Phân số tiếp theo: \(\frac{5}{6}\)
II)
\(\frac{1}{8},\frac{5}{24},\frac{7}{24},...\)
Quy đồng: \(\frac{3}{24},\frac{5}{24},\frac{7}{24},...\)
=> Phân số tiếp theo: \(\frac{9}{24}=\frac{3}{8}\)

a) ta có :
\(\Delta'=1^2-\left(-1-m\right)\left(m^2-1\right)=1-\left(-m^2+1-m^3+m\right)=1+m^2-1+m^3-m=m^3+m^2-m=m\left(m^2+m-1\right)\)để phương trình có nghiệm thì \(\Delta\ge0\)
hay \(m\left(m^2+m-1\right)\ge0\)
=> \(\left\{{}\begin{matrix}m\ge0\\m^2+m-1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}\ge0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2\ge\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left[{}\begin{matrix}m+\dfrac{1}{2}\ge\\m+\dfrac{1}{2}\le-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\dfrac{\sqrt{5}}{2}}\)

ta thấy:\(\dfrac{a}{1+b^2}=a-\dfrac{ab^2}{1+b^2}\)
> áp dụng bđt cosi: 1+b2>=2b
>\(a-\dfrac{ab^2}{1+b^2}\ge a-\dfrac{ab^2}{2b}=a-\dfrac{ab}{2}\)
cminh tương tự với \(\dfrac{b}{1+c^2};\dfrac{c}{1+b^2}\)
cộng lần lượt 2 vế ta vừa cminh
>bthức tương đương với: a+b+c-\(\dfrac{ab+bc+ca}{2}\ge3-\dfrac{3}{2}=\dfrac{3}{2}\) đpcminh
(vì (a+b+c)2>=3(ab+bc+ca) hay 32>=3(ab+bc+ca)
> ab+bc+ca<=3)
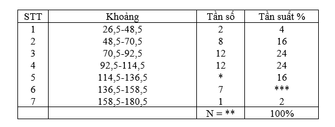

Ta có nhận xét: trong cùng một bảng điều tra; khi 2 giá trị có tần số bằng nhau thì tần suất của chúng cũng bằng nhau và ngược lại
Ta thấy; lớp thứ 5 và lớp thứ 2 có cùng tần suất nên tần số của chúng là bằng nhau.
Do đó; số cần tìm là : 8
Chọn C.