Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

Bạn đổi ra cùng hàm cos rồi lấy máy tính mà bấm cho nhanh :)

Chu kì T = 4s suy ra: \(\omega=2\pi/T=\pi/2(rad/s)\)
Biên độ A1 = 3cm, ban đầu dao động (1) qua VTCB theo chiều dương, suy ra:
\(x_1=3\cos(\dfrac{\pi}{2}t-\dfrac{\pi}{2})\)
Biên độ A2 = 2cm, ban đầu dao động (2) qua VTCB theo chiều âm, suy ra:
\(x_2=2\cos(\dfrac{\pi}{2}t+\dfrac{\pi}{2})\)
Dao động tổng hợp:
\(x=x_1+x_2=\cos(\dfrac{\pi}{2}t-\dfrac{\pi}{2})\) (cm)

Ta có:
Con lắc thực hiện 100 dao động hết 31,4 (s)
Lại có gốc thời gian là lúc quả cầu có li độ 2cm và đang chuyển động theo chiều dương của trục tọa độ với vận tốc có độ lớn
và

Từ ĐK đầu bài ta có:
tần số dao động riwwng của mạch là:
giải phương trình bâc 2 này ra ta được:

\(x=A\sin(\omega t)+A\cos(\omega t)\)
\(=A\sin(\omega t)+A\sin(\omega t+\dfrac{\pi}{2})\)
\(=2A\sin(\omega t+\dfrac{\pi}{4}).\cos \dfrac{\pi}{4}\)
\(=A\sqrt 2\sin(\omega t+\dfrac{\pi}{4})\)
Vậy biên độ dao động là: \(A\sqrt 2\)
Chọn C.

Phương trình tổng quát: \(x = A\cos(\omega t +\varphi)\)
+ Quãng đường khi vật thực hiện 5 dao động: S = 5.4A = 100 cm \(\Rightarrow\) A = 5cm.
+ Tần số: f = 5/2 = 2,5 Hz \(\Rightarrow \omega = 2\pi f = 2\pi.2,5 = 5\pi \ (rad/s)\)
+ t= 0 khi vật có x0=5 nên vật đang ở biên độ dương \(\Rightarrow \varphi = 0\)
Vậy phương trình dao động: \(x=5\cos(5\pi t) \ (cm)\)




 D
D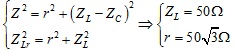
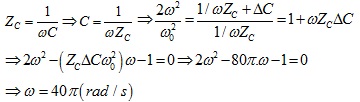
Đáp án D
Từ đồ thị ta viết được phương trình dao động của hai vật:
Sử dụng máy tính cộng số phức ta được phương trình của dao động tổng hợp là:
Các đáp án đều cho biết ω = π/2 rad/s. Hoặc có thể dựa vào trục thời gian để xác định chu kì => tần số góc.