Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{x^7+x^6+x^5+x^4+x^3+x^2+x+1}{x^2-1}\)
\(=\dfrac{x^6\left(x+1\right)+x^4\left(x+1\right)+x^2\left(x+1\right)+\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{\left(x+1\right)\left(x^6+x^4+x^2+1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{x^4\left(x^2+1\right)+\left(x^2+1\right)}{x-1}=\dfrac{\left(x^2+1\right)\left(x^4+1\right)}{\left(x-1\right)}\)
Chúc bạn học tốt!!!

Gọi phân thức cần tìm là \(A\)
Ta có:
\(\dfrac{1}{x}.\dfrac{x}{x+1}.\dfrac{x+1}{x+2}.\dfrac{x+2}{x+3}.\dfrac{x+3}{x+4}.\dfrac{x+4}{x+5}.\dfrac{x+5}{x+6}.\dfrac{x+6}{x+7}.\dfrac{x+7}{x+8}.\dfrac{x+8}{x+9}.\dfrac{x+9}{x+10}\)
\(=\dfrac{x\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)\left(x+6\right)\left(x+7\right)\left(x+8\right)\left(x+9\right)}{\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)\left(x+6\right)\left(x+7\right)\left(x+8\right)\left(x+9\right)\left(x+10\right)}\)\(=\dfrac{x}{x+10}\)
Suy ra:
\(\dfrac{1}{x}.\dfrac{x}{x+1}.\dfrac{x+1}{x+2}.\dfrac{x+2}{x+3}.\dfrac{x+3}{x+4}.\dfrac{x+4}{x+5}.\dfrac{x+5}{x+6}.\dfrac{x+6}{x+7}.\dfrac{x+7}{x+8}.\dfrac{x+8}{x+9}.\dfrac{x+9}{x+10}.A=1\)
\(\Leftrightarrow\dfrac{x}{x+10}.A=1\)
\(\Leftrightarrow A=\dfrac{x+10}{x}\)
Vậy phân thức cần điền vào chỗ trống là \(\dfrac{x+10}{x}\)

Gọi phân thức cần tìm là \(\dfrac{a}{b}\)
Theo đề bài ta có :
\(\dfrac{x}{x+1}:\dfrac{x+2}{x+1}:\dfrac{x+3}{x+2}:\dfrac{x+4}{x+3}:\dfrac{x+5}{x+4}:\dfrac{a}{b}=1\)
\(\Leftrightarrow\dfrac{x}{x+1}\cdot\dfrac{x+1}{x+2}\cdot\dfrac{x+2}{x+3}\cdot\dfrac{x+3}{x+4}\cdot\dfrac{x+4}{x+5}\cdot\dfrac{b}{a}=1\)
\(\Leftrightarrow\dfrac{x}{x+5}\cdot\dfrac{b}{a}=1\)
\(\Rightarrow\dfrac{b}{a}=\dfrac{x+5}{x}\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{x}{x+5}\)
Vậy phân thức cần tìm là \(\dfrac{x}{x+5}\)

\(\frac{x^{10}-x^8-x^7+x^6+x^6+x^4-x^3-x^2+1}{x^{30}+x^{24}+x^{18}+x^{12}+x^6+1}=\frac{(x^{10}-x^8+x^6)-(x^7-x^5+x^3)+(x^4-x^2+1)}{ (x^{30}+x^{18}+x^{24})+(x^{12}+x^6+1)} \)
=\(\frac{(x^4-x^2+1)(x^6-x^3+1)}{(x^{12}+x^6+1)(x^{18}+1 )}=\frac{(x^4-x^2+1)(x^6-x^3+1)}{(x^{12}+2x^6+1-x^6) (x^6+1)(x^{12}-x^6+1)}=\frac{(x^4-x^2+1)(x^6-x^3+1)}{ (x^6-x^3+1)(x^6+x^3+1)(x^2+1)(x^4-x^2+1)(x^12-x^6+1 )} \)
=\(\frac{1}{(x^6+x^2+1)(x^2+1)(x^{12}-x^6+1)}\)

a,\(A=\frac{6x+12}{\left(x+2\right)\left(2x-6\right)}=\frac{6\left(x+2\right)}{2\left(x+2\right)\left(x-3\right)}=\frac{3}{x-3}\)
b, Giá trị của x để phân thức có giá trị bằng (-2) :
\(\frac{3}{x-3}=-2\Rightarrow x=1,5\)

\(\dfrac{x}{x+1}:\dfrac{x+2}{x+3}:\dfrac{x+3}{x+4}:\dfrac{x+4}{x+5}:\dfrac{x+5}{x+6}=\dfrac{x}{x+6}\)

\(\frac{x^4+x^3-x^2-2x-2}{x^4+2x^3-x^2-4x-2}=\frac{\left(x^4-x^2-2\right)+\left(x^3-2x\right)}{\left(x^4-x^2-2\right)+\left(2x^3-4x\right)}\)
\(=\frac{\left(x^2-2\right)\left(x^2+1\right)+x\left(x^2-2\right)}{\left(x^2-2\right)\left(x^2+1\right)+2x\left(x^2-2\right)}=\frac{\left(x^2-2\right)\left(x^2+x+1\right)}{\left(x^2-2\right)\left(x^2+2x+1\right)}\)
\(=\frac{x^2+x+1}{\left(x+1\right)^2}\)
\(F\left(x\right)=\frac{x^4+x^3-x^2-2x-2}{x^4+2x^3-x^2-4x-2}\)
\(=\frac{\left(x^4+x^3+x^2\right)-2x^2-2x-2}{\left(x^4+2x^3+x^2\right)-\left(2x^2+4x+2\right)}\)
\(=\frac{x^2\left(x^2+x+1\right)-2\left(x^2+x+1\right)}{x^2\left(x^2+2x+1\right)-2\left(x^2+2x+1\right)}=\frac{x^2+x+1}{x^2+2x+1}\)
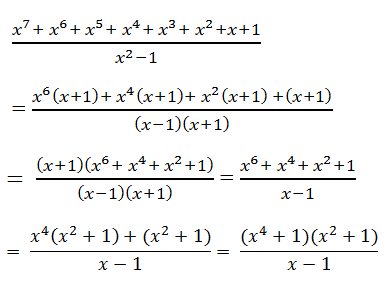
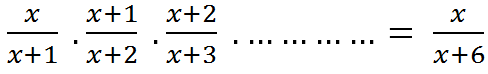
Ta có :\(\frac{x^7+x^6+x^5+x^4+x^3+x^2+1}{x^2-1}\)
\(=\frac{x^6\left(x+1\right)+x^4\left(x+1\right)+x^2\left(x+1\right)+\left(x+1\right)}{x^2-1}\)
\(=\frac{\left(x^6+x^4+x^2+1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{\left(x^6+x^4+x^2+1\right)}{\left(x-1\right)}\)