Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

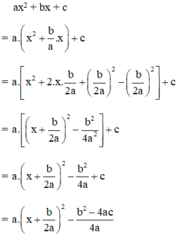
Ta có: a > 0 (gt), 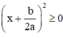 với mọi x, a, b ⇒
với mọi x, a, b ⇒ 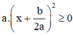
Phương trình ax2 + bx + c = 0 vô nghiệm nên
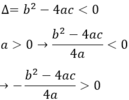
Vậy
a
x
2
+
b
x
+
c
= 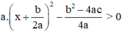 với mọi x.
với mọi x.

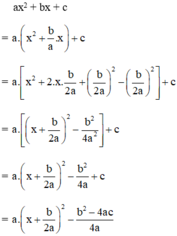
Ta có: a > 0 (gt), 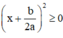 với mọi x, a, b ⇒
với mọi x, a, b ⇒ 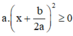
Phương trình ax2 + bx + c = 0 vô nghiệm nên
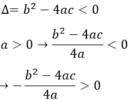
Vậy ax2 + bx + c = 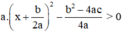 với mọi x.
với mọi x.

Theo đầu bài có \(x_1\)là nghiệm của phương trình \(ax^2+bx+c=0\)nên có
\(ax_1^2+bx_1+c=0\)
chia hai vế cho \(x_1^2\ne0\)ta được \(a+b\frac{1}{x_1}+c\frac{1}{x_1^2}=0\)
ta có \(c.\left(\frac{1}{x_1}\right)^2+b\left(\frac{1}{x_1}\right)+a=0\)
suy ra \(\frac{1}{x_1}\)là nghiệm của của phương trình \(cx^2+bx+a=0\)
Ta chọn \(x_2=\frac{1}{x_1}>0.\)vậy \(x_1x_2=1\)
áp dụng bất đẳng thức Co-si cho 2 hai số dương ta có :
\(x_1+x_2+x_1x_2=x_1+\frac{1}{x_1}+1\ge2\sqrt{x_1.\frac{1}{x_1}}+1=3\left(dpcm\right)\)

Nếu \(b>a+c\)tương đương với \(b^2>a^2+2ac+c^2\)
Trừ cả 2 vế cho 4ac ta được : \(b^2-4ac>a^2-2ac+c^2=\left(a-c\right)^2\)
Hay \(\Delta>\left(a-c\right)^2\ge0\)
Vậy ta có điều phải chứng mình

Câu hỏi của Trần Hà My - Toán lớp 9 - Học toán với OnlineMath
Bạn tham khảo link này nhé!
Khi a > 0 và phương trình vô nghiệm thì b2 – 4ac < 0.
Do đó: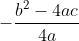 > 0
> 0
Suy ra: ax2 + bx + c = a
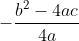 > 0, với mọi x.
> 0, với mọi x.
Nhưng vì sao lại ra được cái dòng cuối vậy bạn