Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

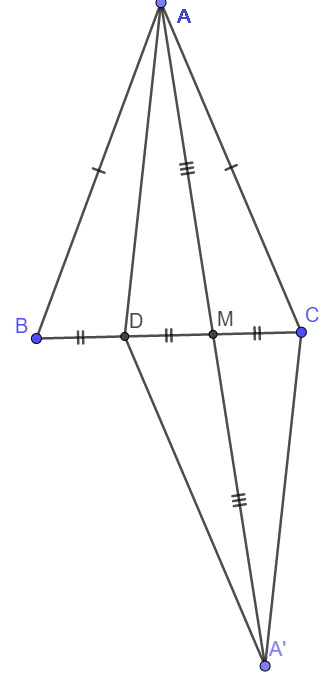
Gọi M là trung điểm DC và A' là điểm thuộc tia AM sao cho AM = MA'.
Khi đó ta thấy ngay \(\Delta AMC=\Delta A'MD\left(c-g-c\right)\)
\(\Rightarrow\widehat{MAC}=\widehat{MA'D}\) và AC = A'D.
Ta cũng có ngay \(\Delta ABD=\Delta ACM\left(c-g-c\right)\Rightarrow\widehat{BAD}=\widehat{CAM}\) và AB = AC
Kẻ AH vuông góc BC. Do tam giác ABC cân nên AH đồng thời là trung tuyến.
Vậy thì ta thấy ngay DH < BH nên theo quan hệ giữa đường xiên và hình chiếu ta có AD < AB
Suy ra AD < AC hay AD < DA'
Xét tam giác ADA' có AD < DA' nên theo quan hệ giữa cạnh và góc trong tam giác ta có :
\(\widehat{DAM}>\widehat{DA'M}\Rightarrow\widehat{DAM}>\widehat{MAC}\)
Lại có \(\widehat{DAM}+\widehat{MAC}=\widehat{CAD}\) nên \(\widehat{MAC}< \frac{1}{2}\widehat{CAD}\)
Vậy thì \(\widehat{BAD}< \frac{1}{2}\widehat{CAD}\left(đpcm\right)\)

Em tham khảo bài tương tự tại đây nhé.
Câu hỏi của Lê Tự Nhật Thạch - Toán lớp 7 - Học toán với OnlineMath
Cho tam giác ABC cân. Trên cạnh đáy BC lấy điểm D sao cho CD = 2BD. So sánh số đo hai góc BAC và CAD

Em tham khảo bài tương tự tại đây nhé.
Câu hỏi của Lê Tự Nhật Thạch - Toán lớp 7 - Học toán với OnlineMath

hình tự kẻ nha
a, XÉT \(\Delta BDC\), có I , M là TĐ của CD , BC
\(\Rightarrow\)IM là đường trung bình của tg BDC
\(\Rightarrow\)IM = 1/2 BD (t/c đg trung bình )
Xét tg CDE có N là TĐ của DE
I là TĐ của CD
\(\Rightarrow\)NI là đường trung bình của tg CDE
\(\Rightarrow\)NI = 1/2 CE (t/c đg trung bình )
Ta có BD = CE (gt)
NI=1/2 CE
MI = 1/2BD
\(\Rightarrow\)NI = MI
\(\Rightarrow\Delta NIM\)cân tại I
b, Xét \(\Delta CBD\),có MI là đường trung bình
\(\Rightarrow\)MI // AB (t/c đường trung bình )
\(\Rightarrow\)\(\widehat{NMI}=\widehat{APQ}\)( so le trong) (1)
\(\Delta CDE\), có NI là đường trung bình
\(\Rightarrow\)NI // AC (t/c đường trung bình)
\(\Rightarrow\)\(\widehat{MNI}=\widehat{MQC}\)( đồng vị)
mà \(\widehat{MQC}=\widehat{AQP}\)(đối đỉnh )
\(\Rightarrow\widehat{MNI}=\widehat{AQP}\) (2)
\(\Delta MNI\)cân tại I \(\Rightarrow\widehat{INM}=\widehat{IMN}\) (3)
từ (1) , (2) và (3) \(\Rightarrow\widehat{APQ}=\widehat{AQP}\)
\(\Rightarrow\Delta APQ\) cân tại A
c, Gọi AD là tia p/g của góc BAC \(\Rightarrow2\widehat{DAC}=\widehat{BAC}\)( tính chất tia p/g) (*)
xét \(\Delta APQ\)có \(\widehat{BAC}=\widehat{APQ}+\widehat{AQP}\)(tính chất góc ngoài)
mà góc APQ = góc AQP suy ra góc BAC= \(\widehat{2AQP}\)(**)
từ (*) và (**) \(\Rightarrow\widehat{DAC}=\widehat{AQP}\)
Mà 2gocs trên lại ở vị trí so le trong của AD và PM
\(\Rightarrow AD//PM\)
\(\Rightarrow\) MN // vs tia p/g của góc A trong tg ABC
#mã mã#

a, Vì △ABC cân tại A (gt) => AB = AC và ABC = ACB
Ta có: ABC + ABE = 180o (2 góc kề bù) và ACB + ACN = 180o (2 góc kề bù)
=> ABE = ACN
Xét △ABE và △ACN
Có: AB = AC (cmt)
ABE = ACN (cmt)
BE = CN (gt)
=> △ABE = △ACN (c.g.c)
=> AE = AN (2 cạnh tương ứng)
=> △AEN cân tại A
b, Xét △HBE vuông tại H và △KCN vuông tại K
Có: BE = CN (gt)
HEB = KNC (△ABE = △ACN)
=> △HBE = △KCN (ch-gn)

a: Xét ΔABE và ΔACDcó
AB=AC
góc BAE chung
AE=AD
=>ΔABE=ΔACD
=>BE=CD
b: ΔABE=ΔACD
=>góc ABE=góc ACD
c: góc ABE+góc KBC=góc ABC
góc ACD+góc KCB=góc ACB
mà góc ABE=góc ACD và góc ABC=góc ACB
nên góc KBC=góc KCB
=>KB=KC
d: AB=AC
KB=KC
=>AK là trung trực của BC
=>A,K,I thẳng hàng