Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
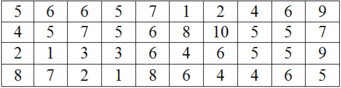
Bảng phân bố tần số - tần suất
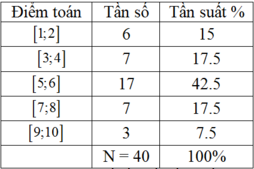
Dựa vào bảng phân bố tần số; tần suất trên ta thấy có 3 lớp có tần suất không bé hơn 17,5% là lớp thứ 2;3 và lớp thứ 4.

Chọn A.
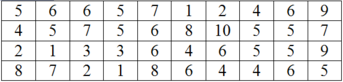
Bảng phân bố tần số - tần suất
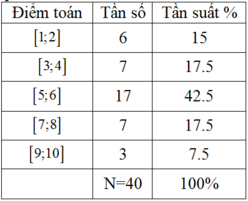
Dựa vào bảng trên ta thấy lớp 3 có tần số và tần suất cao nhất; lớp 5 có tần số; tần suất thấp nhất.
Lớp 2 và 4 có cùng tần số và tần suất.

Tham khảo:
n=10
Giả sử sau khi sắp xếp 10 số dương theo thứ tự không giảm thì được:

=> Trung vị là giá trị trung bình của số thứ 5 và thứ 6.
=> \({Q_1}\) là số thứ 3 và \({Q_3}\) là số thứ 8.
a) Khi nhân mỗi giá trị của mẫu số liệu với 2 thì:
+ Số lớn nhất tăng 2 lần và số nhỏ nhất tăng 2 lần
=> R tăng 2 lần
+ \({Q_1}\) và \({Q_3}\) tăng 2 lần
=> Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\) tăng 2 lần.
+ Giá trị trung bình tăng 2 lần
=> Độ lệch của mỗi giá trị so với giá trị trung bình \(\left| {{x_i} - \overline x} \right|\) cũng tăng 2 lần
=> \({\left( {{x_i} - \overline x} \right)^2}\) tăng 4 lần
=> Phương sai tăng 4 lần
=> Độ lệch chuẩn tăng 2 lần.
Vậy R tăng 2 lần, khoảng tứ phân vị tăng 2 lần và độ lệch chuẩn tăng 2 lần.
b) Cộng mỗi giá trị của mẫu số liệu với 2 thì
+ Số lớn nhất tăng 2 đơn vị và số nhỏ nhất tăng 2 đơn vị
=> R không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ \({Q_1}\) và \({Q_3}\) tăng 2 đơn vị
=> Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\) không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ Giá trị trung bình tăng 2 đơn vị
=> Độ lệch của mỗi giá trị so với giá trị trung bình \(\left| {{x_i} - \overline x} \right|\) không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
=> \({\left( {{x_i} - \overline x} \right)^2}\) không đổi
=> Phương sai không đổi.
=> Độ lệch chuẩn không đổi.
Vậy khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn đều không đổi.

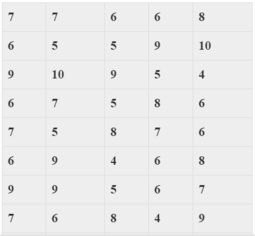
Ta lập bảng phân bố tần số ghép lớp:
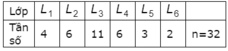
Số học sinh có số điểm trong nửa khoảng [50;80) là 6 + 11 + 6 = 23.


Nhận xét: Số trung bình cộng điểm thi Toán của lớp 10A cao hơn lớp 10B nên có thể nói lớp 10A có kết quả thi môn Toán tốt hơn lớp 10B.

'''''''''''''F'F'S'JURSMJHYT,JTHDNHTDNMYHJFGJHTMJHTMJYT

Đơn vị điều tra: một hsinh lớp 10.
Do lớp học có 22 nữ và 20 nam nên lớp có tất cả 42 học sinh . Do đó; kích thước của mẫu số liệu: 42
Chọn D

Chọn A.
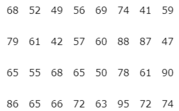
Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A
Liệt kê số điểm của 44 học sinh lớp 10A nên kích thước mẫu của số liệu là 44.

Sắp xếp lại:
5 | 31 | 37 | 43 | 43 | 57 | 62 | 63 | 78 | 80 | 91 |
Khoảng biến thiên R=91-5=86
Ta có: \({Q_2} = 57,{Q_1} = 37,{Q_3} = 78\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 78 - 37 = 41\)
Số trung bình \(\overline X \approx 53,64\)
Ta có bảng sau:
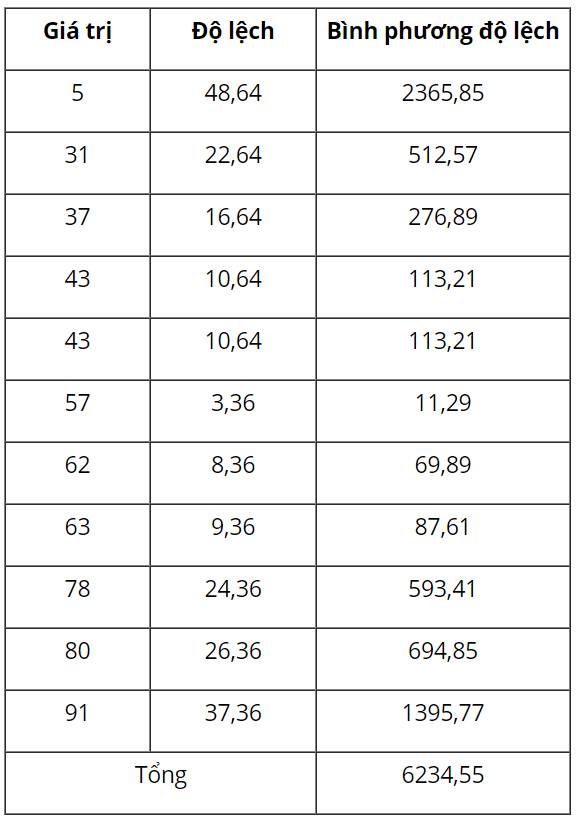
Độ lệch chuẩn là 79
Môn Tiếng Anh:
Sắp xếp lại:
37 | 41 | 49 | 55 | 57 | 62 | 64 | 65 | 65 | 70 | 73 |
Khoảng biến thiên R=73-37=36
Ta có: \({Q_2} = 62,{Q_1} = 49,{Q_3} = 65\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 65 - 49 = 16\)
Số trung bình \(\overline X = 58\)
Ta có bảng sau:
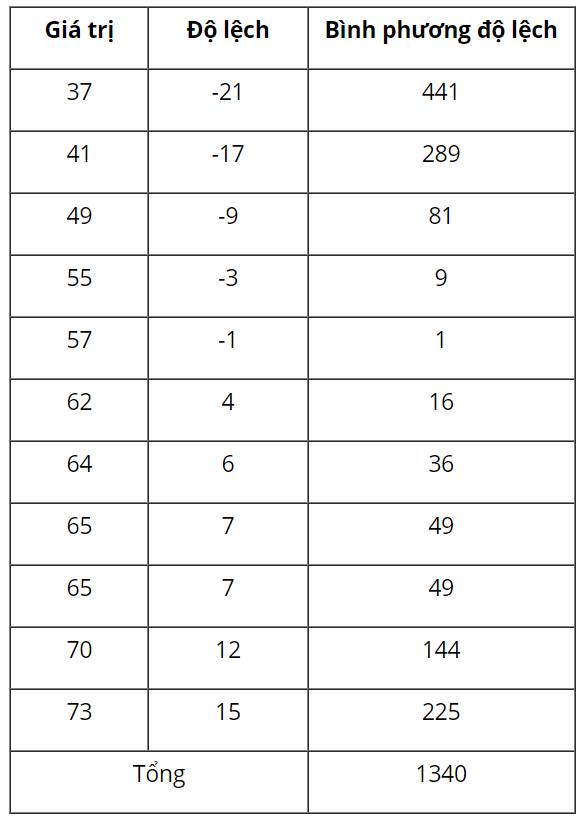
Độ lệch chuẩn là 36,6
Từ các số trên ta thấy mức độ học tập môn Tiếng Anh không đều bằng môn Toán.Độ lệch chuẩn là 36,6

Ta có n=2+4+6+12+8+3=35, lẻ.
Trung vị là học sinh thứ 18
Ta thấy 2+4+6<18<2+4+6+12
=> \({Q_2} = 3\)
Ta tìm \({Q_1}\) là trung vị của nửa số liệu bên trái \({Q_2}\)(không bao gồm \({Q_2}\))
Nửa số liệu bên trái \({Q_2}\) có 17 học sinh nên trung vị là học sinh thứ 9:
Ta thấy 2+4<9<2+4+6
=>\({Q_1} = 2\)
Ta tìm \({Q_3}\) là trung vị của nửa số liệu bên phải \({Q_2}\)(không bao gồm \({Q_2}\))
Nửa số liệu bên phải \({Q_2}\) có 17 học sinh nên trung vị là học sinh thứ 9 trong 17 học sinh và là học sinh thứ 9+18=27 trong 35 học sinh.
Ta thấy 2+4+6+12<27<2+4+6+12+8
=>\({Q_3} = 4\)